Ellipses
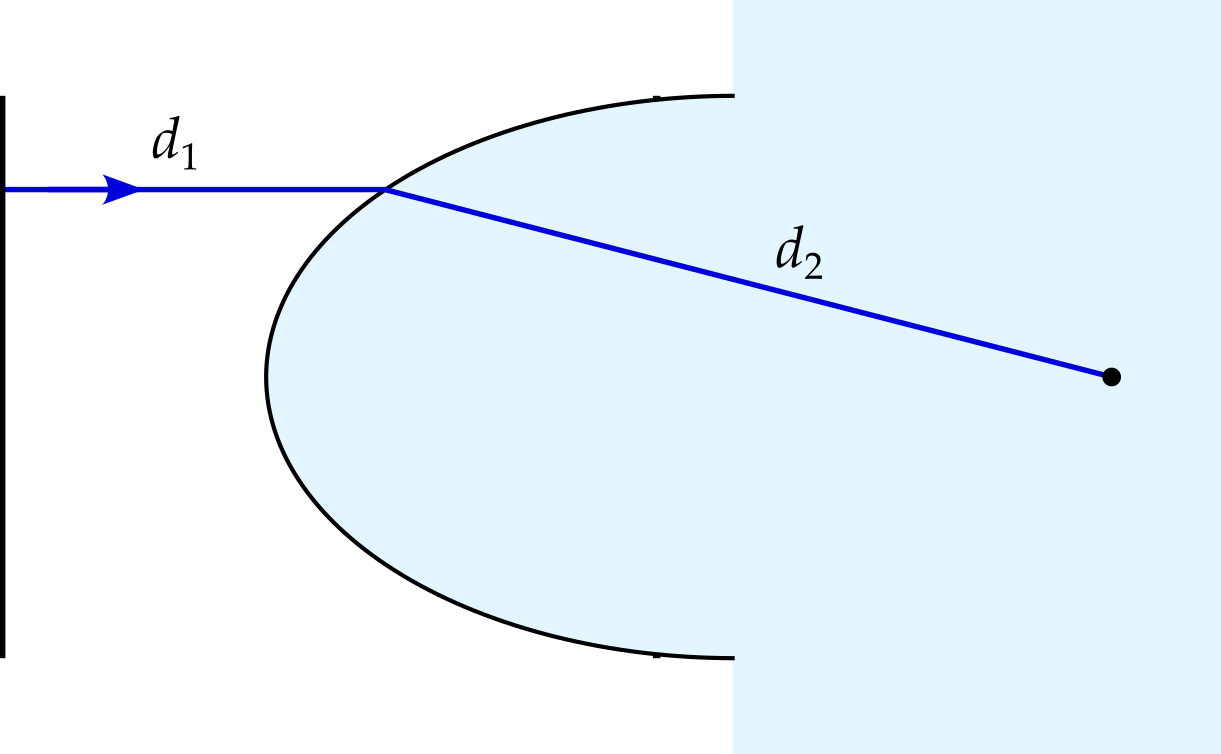
When discussing lenses, we claimed that an ellipse of appropriate eccentricity satisfies the equation \[ n_1d_1 + n_2d_2 = \text{const}, \tag{1}\] where \(d_1\) is the distance of a point on the ellipse to a vertical line and \(d_2\) is the distance from the point to one of the foci. Here we will check that this is the case.
Two definitions
There are at least four common definitions of an ellipse — we will need two.
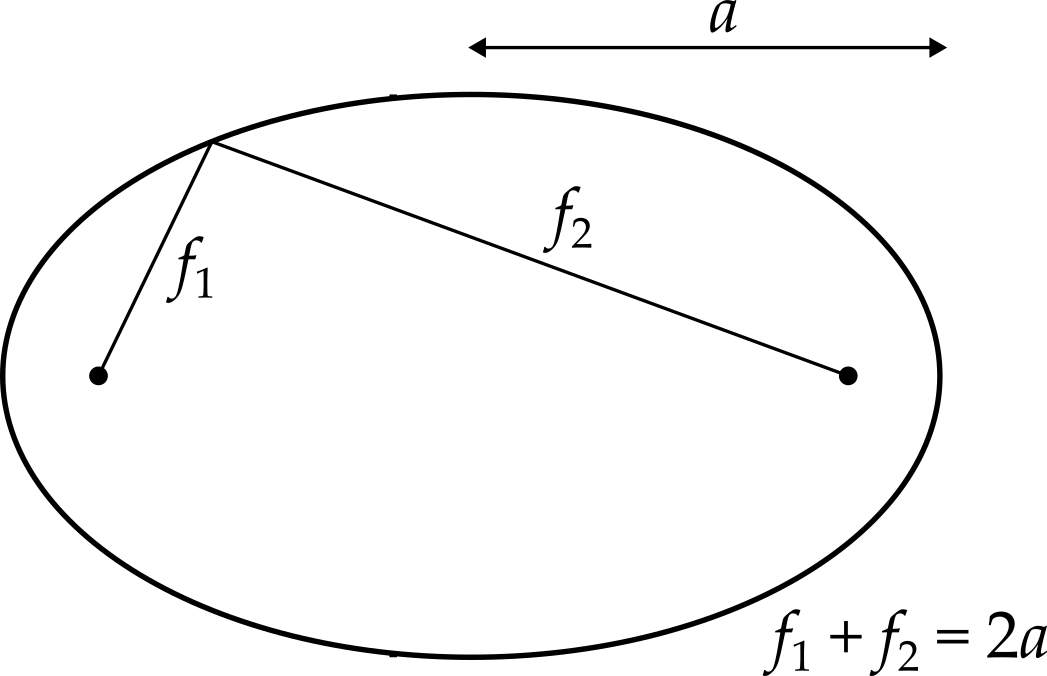
Sum of distances: Given two fixed points (the foci) and a constant \(2a\), find the set of points such that the sum of distances to each focus equals \(2a\). These points form an ellipse.1
1 Here \(a\) is the length of the semi-major axis — the line from the centre of the ellipse to its furthest point.
Directrix and focus: Given a straight line (called the directrix) and a number \(e\) (the eccentricity) between zero and one, find the set of points such that the ratio of the distance to the focus and the distance to the directrix equals \(e\). These points form an ellipse.

Deriving a condition on \(d\) and \(f_2\)
How are \(d\) and \(f_2\) related? Taking the two definitions, we can eliminate \(f_1\) to get \[ de + f_2 = 2a. \] To relate this to the discussion on lenses, multiply by \(n_1 / e\) to get \[ n_1d + \frac{n_1}{e}f_2 = \frac{2n_1a}{e}. \] Furthermore, to relate to figure 1, let \(d = d_1\) and \(f_2 = d_2\), to get \[ n_1d_1 + \frac{n_1}{e}d_2 = \frac{2n_1a}{e}. \] If this is to match equation 1, we require2 \(e = n_1 / n_2\), which produces \[ n_1d_1 + n_2d_2 = 2n_2a. \] The left hand side now matches that of equation 1. The right hand side is a constant, but perhaps not the same constant as in equation 1. This can be fixed by simply moving the vertical line.
2 Note that this rules out a circular/spherical surface, since the eccentricity of a circle is zero.
We have therefore discovered that an ellipse (or ellipsoid in three dimensions) of eccentricity \(e = n_1 / n_2\) is the correct shape for the interface between air and glass to focus parallel light rays to a single point. Notice that larger ellipses, of the same eccentricity, produce longer focal lengths. It may not be necessary to use the entire ellipse — if we wish to focus a narrow beam of rays to a distant focal point, only the central portion of the ellipse (or ellipsoid) is required.