3  Polarisation

3.1 Longitudinal and transverse waves

When considering waves through a medium, e.g. sound through the air or waves in a spring, the wave is longitudinal if the displacement of the medium is along the direction of the wave.

Figure 3.1: A longitudinal wave. (Courtesy of Andrew McKinley.)

If the displacement is perpendicular to the direction of propagation then we have a transverse wave.

Figure 3.2: A transverse wave. (Courtesy of Andrew McKinley.)

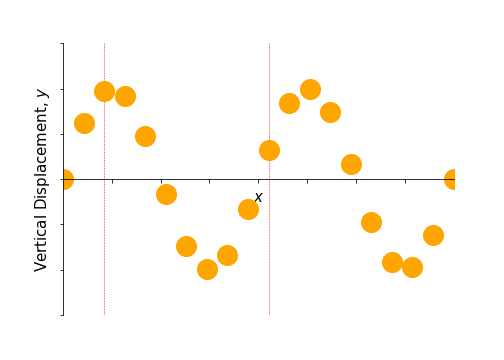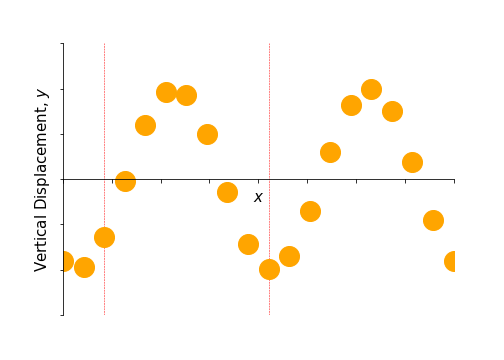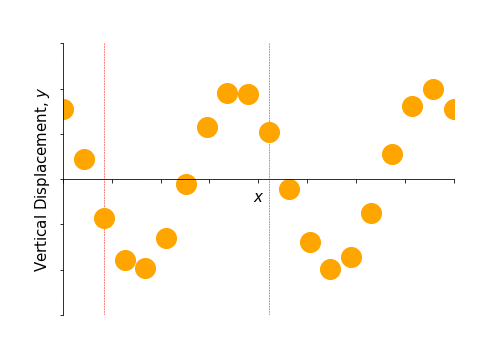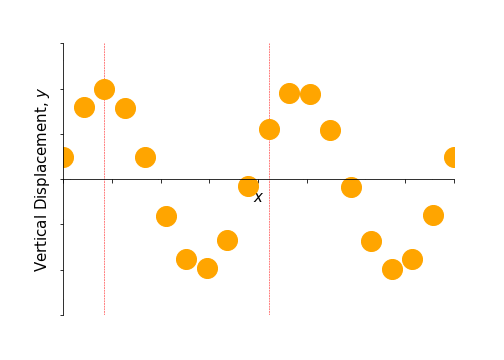
3.2 Linear polarisation

Imagine a transverse wave propagating along a string. At each point in the string, there is an entire two dimensional space perpendicular to the string into which that point can be displaced. That is, there are different directions of polarisation. Two examples are vertical polarisation and horizontal polarisation, illustrated in figures 3.3 and 3.4. Using the complex representation, such waves might be given by \[ \mathbf{f}_\text{v}(x, t) = Ae^{i(kx-\omega t)}\hat{\mathbf{y}} \] and \[ \mathbf{f}_\text{h}(x, t) = Ae^{i(kx-\omega t)}\hat{\mathbf{z}} \] respectively.

Figure 3.3: Vertical polarisation

Figure 3.4: Horizontal polarisation

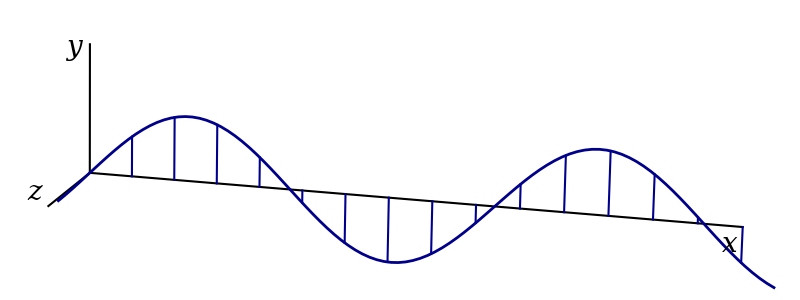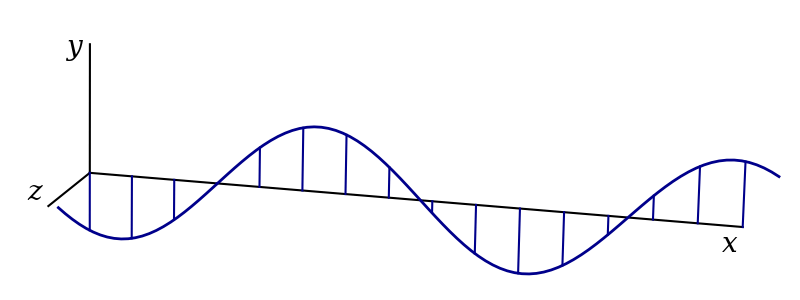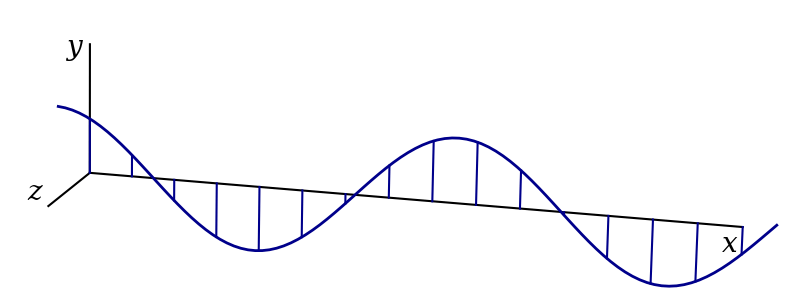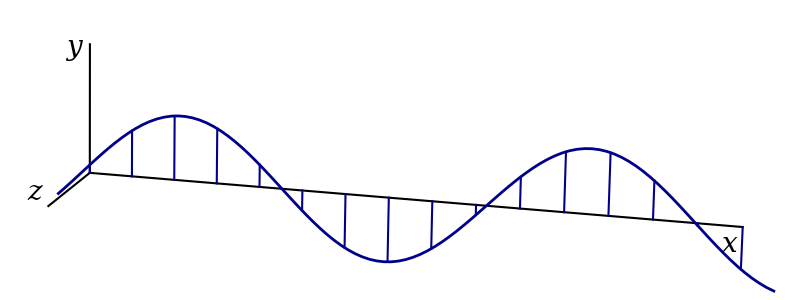
These are both forms of linear polarisation. Assuming that the wave is following a linear differential equation, we can add these solutions to produce another. This new wave, given by \[ \mathbf{f}_{45}(x, t) = \mathbf{f}_\text{h}(x, t) + \mathbf{f}_\text{v}(x, t) = Ae^{i(kx-\omega t)}\left(\hat{\mathbf{y}} + \hat{\mathbf{z}}\right), \] is linearly polarised in a direction at 45 degrees to the \(y\) and \(z\) axes and is shown in figure 3.5

Figure 3.5: Polarisation at 45 degrees

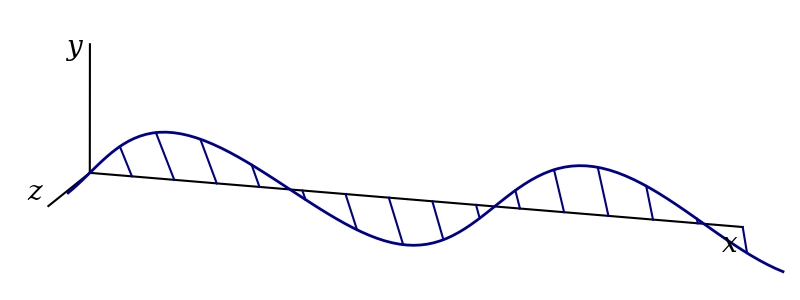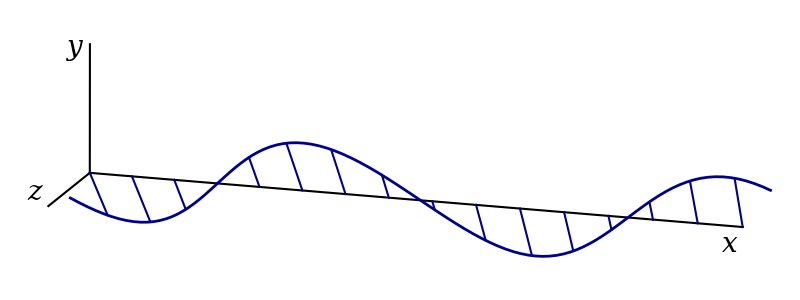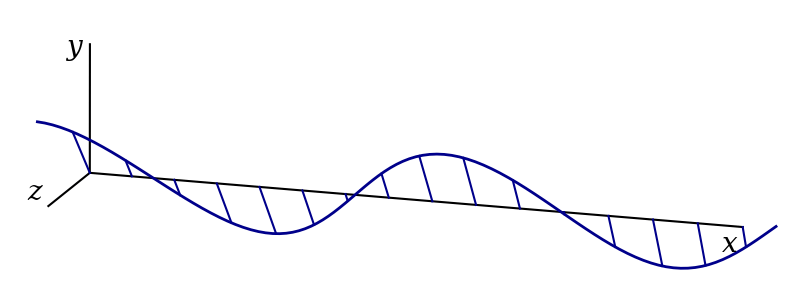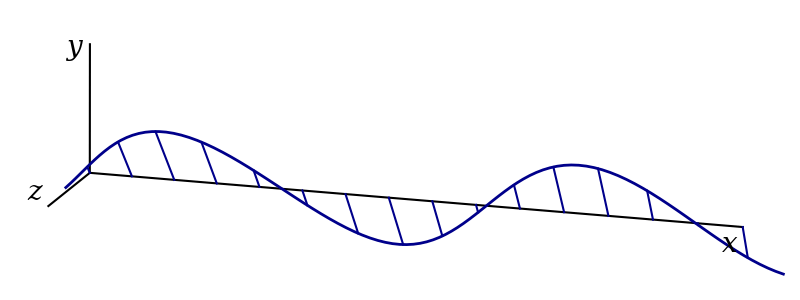
Indeed, if we define a polarisation angle, \(\theta\), we can arrange for the wave to be linearly polarised in any direction, \(\hat{\mathbf{n}} = \hat{\mathbf{z}}\cos\theta + \hat{\mathbf{y}}\sin\theta\), perpendicular to the \(x\)-axis by choosing the solution \[ \begin{aligned} \mathbf{f}(x, t) &= \mathbf{f}_\text{h}(x, t)\cos\theta + \mathbf{f}_\text{v}(x, t)\sin\theta\\ &= Ae^{i(kx - \omega t)}\left(\hat{\mathbf{z}}\cos\theta + \hat{\mathbf{y}}\sin\theta\right)\\ &= Ae^{i(kx - \omega t)}\hat{\mathbf{n}} \end{aligned} \]

3.3 More polarisation

Having polarised the wave in every direction perpendicular to the direction of travel, one might think that we have exhausted all the possibilities for polarisation. We haven’t. Thus far we have only added waves that are in phase, meaning that the peaks of the horizontal component coincide with the peaks (or perhaps the troughs) of the vertical component, while when the displacement in the \(y\) direction is zero, so is the displacement in the \(z\) direction. What happens if we now delay the vertically polarised component by a phase difference of \(\pi/2\)?

Figure 3.6: Circular polarisation

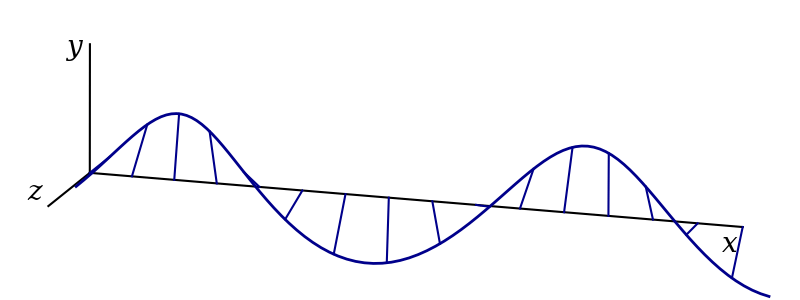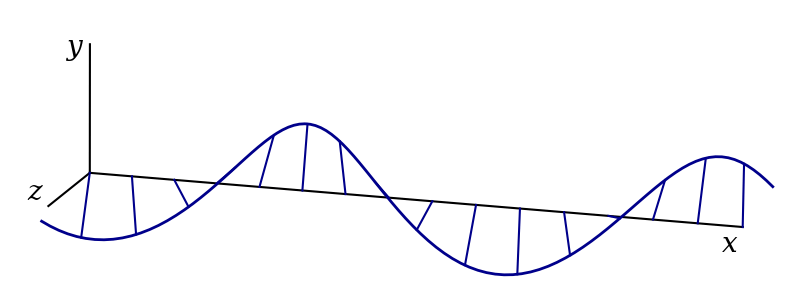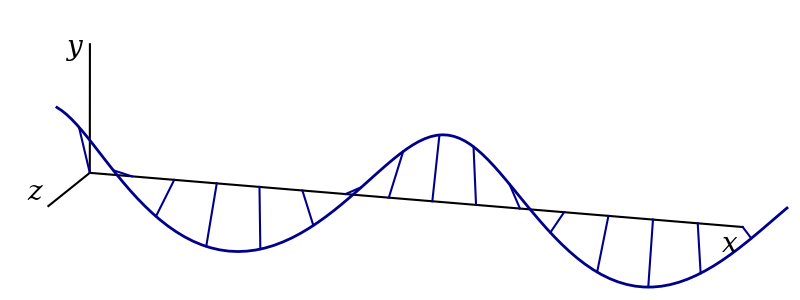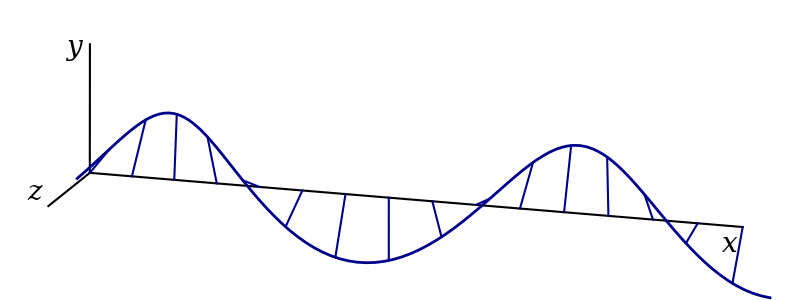
The result is circular polarisation, as shown in figure 3.6. Mathematically, this is given by¹ \[ \begin{aligned} \mathbf{f}(x, t) &= Ae^{i(kx-\omega t + \pi/2)}\hat{\mathbf{y}} + Ae^{i(kx-\omega t)}\hat{\mathbf{z}}\\ &= Ae^{i(kx-\omega t)}\left(i\hat{\mathbf{y}} + \hat{\mathbf{z}}\right)\\ &= i\mathbf{f}_\text{v} + \mathbf{f}_\text{h}. \end{aligned} \]

¹ Notice how, in the complex representation, delaying the wave or a part of the wave can be achieved by simply multiplying by \(e^{i\theta}\), for some \(\theta\). Confusingly, \(e^{i\theta}\) is often referred to as a phase factor.

Circularly polarised waves can be left-handed (anticlockwise) as shown, or right-handed (clockwise). Furthermore, further adjustments to the amplitudes of the horizontal and vertical components and to the timing can produce various forms of elliptical polarisation.

3.4 Unpolarised light

We have finally completed the list of ways in which light can be polarised, but what about unpolarised light. Individual photons² always have some specific polarisation, but a beam of light will consist of many such photons. If each photon’s polarisation is essentially random and independent of the polarisation of the other photons, then the beam is unpolarised.³

² Talking about the polarisation of a particle like sounds strange. Unfortunately, you will have to wait a while before you understand the quantum mechanics of light.

³ This explanation is simplified somewhat, since once we mention photons we enter the realms of quantum mechanics and quantum field theory. Discussing, for example, the polarisation of entangled photons raises complications. Hopefully, though, this gives a broadly correct intuition about the nature unpolarised light.