4  Differentiation

4.1 Introduction

Much of complex analysis is the study of differentiable (or holomorphic or analytic1) functions. The definition of the derivative of a complex function, which I will provide soon, should contain few surprises. Moreover, in practice you will seldom use the definition directly, preferring instead to use the rules — chain rule, product rule, etc. — that you are already familiar with and that continue to work for complex functions. So what is new?

1 We will see later that there are subtle differences between the three terms but these differences should be unimportant for much of this course.

The novel features of the derivative arise from the fact that the limit in the definition is now a limit in the complex plane, rather than on the real line. For the derivative to exist at \(z\), this limit must be the same, regardless of the direction in which \(z\) is approached and, in the complex plane, there are infinitely many such directions. This requirement imposes a certain rigidity on a holomorphic complex function.

For example, we may be given a function on a small subset2 of the complex plane and asked to extend the function to cover all of \(\mathbb{C}\). There are infinitely many ways to do this. However, if we are also told that the function must be holomorphic then we find that there is at most one function that will work.

2 Not just any subset will do, but I will ignore the additional requirement for now. If you are interested, look up the details of analytic continuation.

4.2 Definition of the derivative

Definition 4.1 The derivative3 of a complex function, \(f(z)\), is given by \[ f'(z) \equiv \frac{df}{dz} = \lim_{\delta z \rightarrow 0}\frac{f(z + \delta z) - f(z)}{\delta z} \] where this limit exists. When the limit exists, we say that \(f\) is differentiable at \(z\).

3 Technically, we should also require \(f\) to be defined in a neighbourhood of \(z\) before definining the derivative at \(z\). This ensures that \(f(z + \delta z)\) is defined regardless of the direction in which we approach \(z\).

Recall that, for real functions we could define a left limit and a right limit and that the limit only exists if these agree. This suggests that, for real functions, we could similarly define a left derivative and a right derivative, with the derivative only existing if these agree.

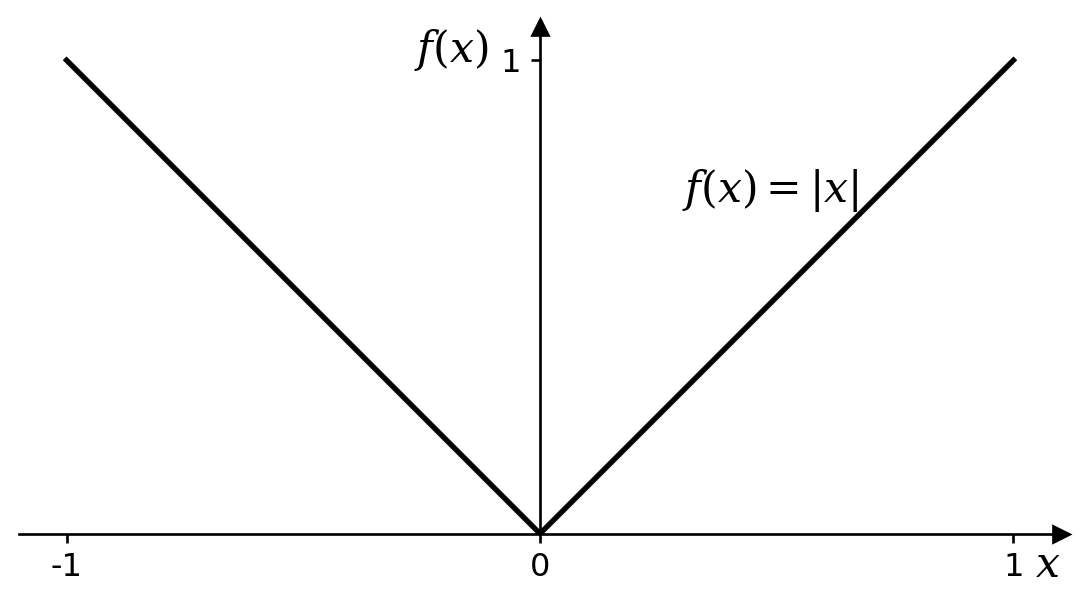
Example 4.1 (A non-differentiable real function) Consider \(f(x) = \left|x\right|\).

A graph of the absolute value of $x$, sloping down at 45 degrees (i.e. a gradient of minus one) for negative $x$ and up at 45 degrees (i.e. a gradient of one) for positive $x$. At $x = 0$ there is an abrupt change of direction in the graph.
Figure 4.1: Graph of the function \(f(x) = \left|x\right|\).

The derivative, \(f'(x)\), is well-defined provided \(x \neq 0\) and equals \(1\) for positive \(x\) and \(-1\) for negative \(x\). We could define left and right derivatives at \(x = 0\), giving values of \(-1\) and \(1\) respectively, but since these do not agree, the derivative is not defined at \(x = 0\).

Since the derivative is not defined at \(x = 0\) for the real function \(f(x) = \left|x\right|\), it is certainly not defined at \(z = 0\) for the complex function \(f(z) = \left|z\right|\) either, since we can still approach \(z = 0\) along the two directions on the real axis. We will see later that the derivative of \(f(z) = \left|z\right|\) is not defined anywhere in the complex plane.

While a real value, \(x\), can be approached in two directions on the real line — from above or from below — a complex number, \(z\), can be approached in infinitely many directions on the complex plane. The fact that the derivative has to be the same, regardless of the direction taken, will have far-reaching consequences.

The point $z = 1 + i$ plotted on the complex plane with eight arrows approaching it.
Figure 4.2: Just some of the infinitely many directions in which to approach \(z = 1 + i\) in the complex plane.

4.3 The Cauchy-Riemann equations

We will consider calculating the limit by approaching \(z\) in the purely imaginary (vertical) direction and in the purely real (horizontal) direction and see how this constrains the form of a differentiable function, \(f\). However, before we do this, we will consider both \(z\) and \(f(z)\) in terms of their real and imaginary components.

We let the input, \(z\), to the function be equal to \(x + iy\), where both \(x\) and \(y\) are real4. We also write \(\delta z = \delta x + i\delta y\). Similarly, we let the output, \(f(z)\), equal \(u + iv\). We can think of \(u\) and \(v\) as being real valued functions of two real variables, \(x\) and \(y\), i.e. \(u = u(x, y)\) and \(v = v(x, y)\). Again, we write \(\delta f = \delta u + i\delta v\). We assume that partial derivatives of \(u\) and \(v\) both exist, otherwise there would be no hope of finding a complex derivative.

4 In other words, define \(x = \operatorname{Re}z\) and \(y = \operatorname{Im}z\).

If the derivative, \(f'(z)\), exists, then we can find it by fixing \(\delta y = 0\) and letting \(\delta x\) approach zero. Let’s do that:

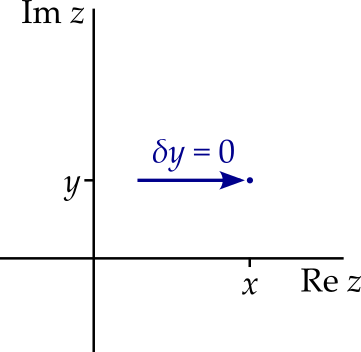
Point $x + iy$ plotted on the complex plane, with an arrow approaching from the left.
Figure 4.3: Calculating \(f'(z)\) by varying only the real part of \(z\). (Note that, in our calculation we actually consider approaching from both the left and from the right simultaneously. That is, we calculate the derivative along a horizontal line.)

\[ \frac{df}{dz} = \lim_{\delta z \rightarrow 0}\frac{f(z + \delta z) - f(z)}{\delta z} = \lim_{\delta z \rightarrow 0}\frac{\delta u + i\delta v}{\delta x + i\delta y}. \] Fixing \(\delta y = 0\) we get \[ \begin{aligned} \frac{df}{dz} &= \lim_{\delta x \rightarrow 0}\frac{\delta u}{\delta x} + i\lim_{\delta x \rightarrow 0}\frac{\delta v}{\delta x}\\ &= \frac{\partial u}{\partial x} + i\frac{\partial v}{\partial x}. \end{aligned} \]

Let’s also calculate the derivative (if it exists) by taking the limit in the imaginary direction, i.e. by fixing \(\delta x = 0\) and letting \(\delta y\) approach zero. Now we get

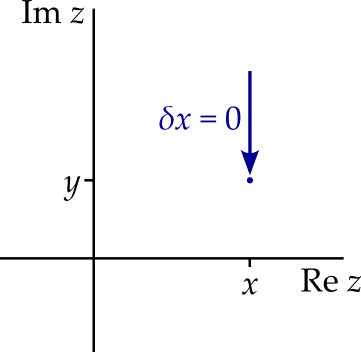
Point $x + iy$ plotted on the complex plane, with an arrow approaching from above.
Figure 4.4: Calculating \(f'(z)\) by varying only the imaginary part of \(z\). (In our calculation we actually consider approaching from both above and below simultaneously. That is, we calculate the derivative along a vertical line.)

\[ \begin{aligned} \frac{df}{dz} &= \lim_{\delta y \rightarrow 0}\frac{\delta u}{i\delta y} + \lim_{\delta y \rightarrow 0}\frac{i\delta v}{i\delta y}\\ &= -i\lim_{\delta y \rightarrow 0}\frac{\delta u}{\delta y} + \lim_{\delta y \rightarrow 0}\frac{\delta v}{\delta x}\\ &= -i\frac{\partial u}{\partial y} + \frac{\partial v}{\partial y}. \end{aligned} \] For the derivative to exist, these two expressions must be equal. Equating the real parts and the complex parts, we get the Cauchy-Riemann equations \[ \boxed { \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}\qquad \text{and} \qquad \frac{\partial v}{\partial x} = -\frac{\partial u}{\partial y}. } \]

We have shown that the Cauchy-Riemann conditions are necessary, if our function is to be differentiable. It is also possible to show that if the Cauchy-Riemann conditions hold at \(z\) and the partial derivatives are continuous in a neighbourhood of \(z\), then function \(f\) is differentiable at \(z\).

Example 4.2 \[f(z) = z^2.\] Expanding this in terms of the real and imaginary parts of \(z = x + iy\), we get \[f(x, y) = (x^2 - y^2) + 2ixy.\] Hence the real and imaginary parts of \(f\) are \[ \begin{aligned} u(x, y) &= x^2 - y^2,\\ v(x, y) &= 2xy. \end{aligned} \] Checking the Cauchy-Riemann equations, we find that \[ \begin{aligned} \frac{\partial u}{\partial x} & = 2x = \frac{\partial v}{\partial y},\\ \frac{\partial v}{\partial x} &= 2y = -\frac{\partial u}{\partial y}. \end{aligned} \] Since the Cauchy-Riemann equations check out and the partial derivatives are continuous, \(f(z) = z^2\) is differentiable, with the derivative given by \[ f'(z) = \frac{\partial u}{\partial x} + i\frac{\partial v}{\partial x} = 2x + 2iy = 2z. \]

Notice that the derivative in this example is hardly a surprise — it is exactly what we would have got for the real version of the function. This will also be the case for the complex extensions of the other familiar functions, e.g. \(z^3\), \(1/z\), \(e^z\), \(\sin z\), etc.

Example 4.3 \[f(z) = \operatorname{Im}z\] Expanding in terms of the real and imaginary parts of \(z = x + iy\), this becomes \[f(x, y) = y,\] i.e. \[ \begin{aligned} u(x, y) &= y,\\ v(x, y) &= 0. \end{aligned} \] Checking the Cauchy-Riemann equations, we find that \[ \begin{aligned} \frac{\partial u}{\partial x} & = 0 = \frac{\partial v}{\partial y},\\ \frac{\partial v}{\partial x} &= 0 \neq -1 = -\frac{\partial u}{\partial y}. \end{aligned} \] The Cauchy-Riemann equations never hold, so this function is differentiable nowhere.

Show that the complex function \(f(z) = \left|z\right|\) is differentiable nowhere.

Expanding in terms of the real and imaginary parts of \(z = x + iy\), we get \[ f(x, y) = \sqrt{x^2 + y^2} \] and so \[ \begin{aligned} u(x, y) &= \sqrt{x^2 + y^2},\\ v(x, y) &= 0. \end{aligned} \] Checking the partial derivatives, we find that \[ \frac{\partial u}{\partial x} = \frac{x}{\sqrt{x^2 + y^2}}, \qquad \frac{\partial v}{\partial y} = 0. \] These are only equal if \(x = 0\). Similarly \[ \frac{\partial v}{\partial x} = 0, \qquad -\frac{\partial u}{\partial y} = -\frac{y}{\sqrt{x^2 + y^2}}, \] These are only equal if \(y = 0\). Hence the Cauchy-Riemann conditions fail to hold whenever \(z = x + iy \neq 0\).

At \(z = 0\), the situation is a little more complicated — the partial derivatives have zero divided by zero. However, we already found that \(f(z) = \left|z\right|\) is not differentiable at \(z = 0\) in example 4.1.

4.4 Some terminology

We have defined what it means for a complex function to be differentiable. What does it mean when we use the related terms like holomorphic or analytic.

A function \(f\) is holomorphic at \(z\) if it is differentiable in a neighbourhood of \(z\). It is holomorphic in a region, \(G \subseteq \mathbb{C}\), if it is differentiable at all points in the region. Notice that holomorphism is a stronger condition than differentiability - a function may be differentiable at an isolated point \(z\) but not holomorphic there.

A function \(f\) is analytic in region \(G\) if, for any \(z_0 \in G\), we can construct the Taylor series around \(z_0\) and have it converge to \(f\) in some neighbourhood of \(z_0\). In complex analysis, it turns out that holomorphic functions are analytic and vice-versa, so we may use these terms interchangeably. (You may also find text books that refer to holomorphic functions as being regular.)

Finally, an entire function is one that is differentiable over the whole complex plane.

Determine whether the function \(f(z) = \left|z\right|^2 = zz^*\) is complex differentiable anywhere, and if so, where. Where is it holomorphic?

Writing \(z = x + iy\) and \(f = u + iv\), where \(u\) and \(v\) are both real valued functions of \(x\) and \(y\), we find that \[ \begin{aligned} u(x, y) &= x^2 + y^2\\ v(x, y) &= 0 \end{aligned} \] Checking the Cauchy-Riemann conditions, we find that \[ \frac{\partial u}{\partial x} = 2x, \qquad \frac{\partial v}{\partial y} = 0. \] and these can only be equal when \(x = 0\). Similarly, \[ \frac{\partial v}{\partial x} = 0, \qquad -\frac{\partial u}{\partial y} = -2y. \] and these can only be equal when \(y = 0\). Hence, the only possible place where the function can be differentiable is \(z = 0\).

Given that the Cauchy-Riemann conditions hold at \(z = 0\) and that the partial derivatives are continuous in a neighbourhood of \(z = 0\), we can claim that \(f\) is differentiable at \(z = 0\). Indeed \[ \left.\frac{df}{dz}\right|_{z = 0} = \lim_{\delta z \rightarrow 0}\frac{f(\delta z) - f(0)}{\delta z} = \lim_{\delta z \rightarrow 0}\frac{\delta z\delta z^*}{\delta z} = \lim_{\delta z \rightarrow 0}\delta z^* = 0. \] However, \(f\) is not differentiable in any neighbourhood of \(z = 0\), but only at the isolated point. Hence it is holomorphic nowhere.

4.5 Differentiation of power series

Naturally, calculating derivatives of complex functions from first principles5 becomes tiresome quickly, just as it does for real functions. Just as for real differentiation, when calculating a complex derivative in practice, we use a set of rules - the chain rule, product rule, etc - to construct the answer from derivatives of simpler functions.

5 That is, directly from the definition of the derivative.

I am not going to prove, for example, the chain rule for complex differentiation. Instead, remind yourself of the proof for real functions. Since the definition of the derivative is the same in both cases, this proof will work for complex functions too! Similarly, the derivative of \(f(z) = z^n\) is still \(f'(z) = nz^{n - 1}\) and is found in exactly the same way as for the real case.

Recall, however, that we have redefined some functions, such as the exponential function, in terms of power series. We should perhaps check that the derivatives of these functions are still the same. We will use the following theorem.

Theorem 4.1 If \[ f(z) = \sum_{n = 0}^\infty a_nz^n \] then, within the radius of convergence, \(f\) is differentiable and its derivative can be found by differentiating the series term by term. That is \[ f'(z) = \frac{d}{dz}\sum_{n = 0}^\infty a_nz^n = \sum_{n = 0}^\infty \frac{d}{dz} a_nz^n = \sum_{n = 0}^\infty na_nz^{n - 1} = \sum_{n = 1}^\infty na_nz^{n - 1}. \]

Proof. Omitted.6

6 This is not ‘obvious’. The tricky part is pushing the \(\frac{d}{dz}\) operator through the summation sign. If the sum were a finite sum, then this would be straightforward, but it is an infinite series, which is the limit of a sequence of finite sums. Switching the derivative with the summation sign involves switching two limits and this can be a rather subtle matter.

Show that the derivative of \(f(z) = e^z\) is \(f'(z) = e^z\).

Recall that \(e^z\) is defined as \[ e^z = \sum_{n = 0}^\infty \frac{z^n}{n!}. \] Differentiating term by term, we find that \[ \frac{d}{dz}e^z = \frac{d}{dz}\sum_{n = 0}^\infty \frac{z^n}{n!} = \sum_{n = 0}^\infty\frac{d}{dz}\frac{z^n}{n!} = \sum_{n = 1}^\infty\frac{z^{n - 1}}{(n - 1)!} = \sum_{n = 0}^\infty\frac{z^n}{n!} = e^z. \] The radius of convergence of the power series for \(e^z\) is easily shown to be infinite, so \(e^z\) is differentiable (and hence continuous) everywhere, with derivative \(e^z\).

4.6 Some properties of holomorphic functions

The constraints imposed on holomorphic functions by the Cauchy-Riemann conditions mean that such functions satisfy a number of interesting properties and, in a sense, much of complex analysis is a study of these properties. For example, a holomorphic function is infintely differentiable7 - the existence of a complex derivative in a region implies the existence of the second derivative, third derivative etc. Note how this contrasts with the case for real functions.

7 Not proved here.

Convince yourself that the first derivative of the real function \[ f(x) = \begin{cases} x^2 & x \geq 0\\ -x^2 & x < 0. \end{cases} \] exists at every (real) value of \(x\). Does the second derivative also exist at all values of \(x\)?

The derivative is \[ f(x) = 2\left|x\right| \] for any value of \(x\), including \(x = 0\), where the derivative is zero. However, we have already seen that \(\left|x\right|\) is not differentiable at \(x = 0\). Hence, while the second derivative, \(f''(x)\) exists for all other values of \(x\), it does not exist at \(x = 0\).

4.6.1 Harmonic functions

Perhaps of particular interest to physicists, the real and the imaginary parts of a holomorphic function are automatically harmonic functions, that is, they are smooth solutions to Laplace’s equation, \(\nabla^2\phi = 0\). This is an immediate result of the Cauchy-Riemann conditions.

Let us prove this for the real part \(u(x, y)\) of holomorphic function \(f(z) = u(x, y) + iv(x, y)\), where \(z = x + iy\). Being holomorphic, we can take the Cauchy-Riemann equations \[ \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y},\qquad \frac{\partial v}{\partial x} = -\frac{\partial u}{\partial y}. \] and differentiate the first with respect to \(x\) and the second with respect to \(y\), to get \[ \frac{\partial^2 u}{\partial x^2} = \frac{\partial^2 v}{\partial x\partial y},\qquad \frac{\partial^2 v}{\partial y\partial x} = -\frac{\partial^2 u}{\partial y^2}. \] Since partial derivatives commute, the mixed derivatives here are equal. Hence \[ \frac{\partial^2 u}{\partial x^2} = -\frac{\partial^2 u}{\partial y^2} \] and hence \[ \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0 \] as required

Exercise

Take different derivatives of the Cauchy-Riemann conditions to show a similar result for \(v\).

4.6.2 Conformal mappings

Considered as a transformation of the complex plane, holomorphic functions have the additional property that they describe conformal mappings, except possibly where the derivative is exactly zero. A conformal mapping is a mapping that locally preserves angles, but does not necessarily conserve lengths or curvature.

What does it mean to locally preserve angles? It means that the angle between two paths8 at the point where they meet is preserved by the transformation.

8 We will describe paths in a little more detail prior to describing integration. If this part of the notes does not make sense on your first reading, come back to it after covering paths.

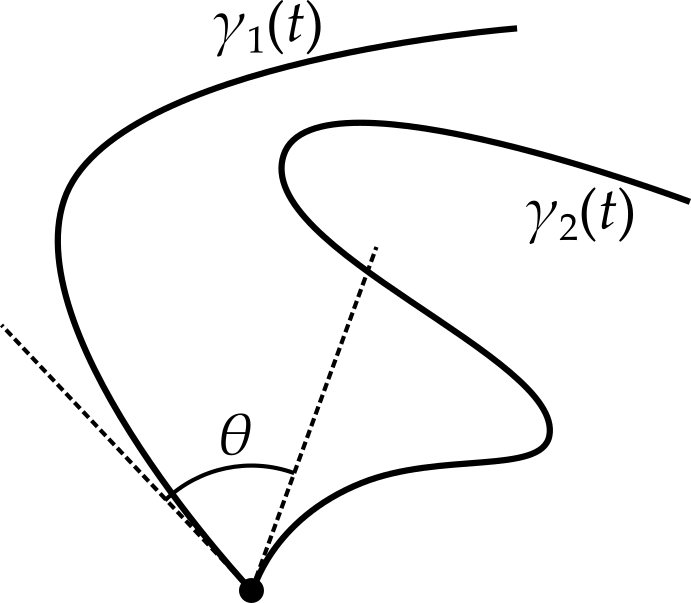
Two paths in the complex plane, starting from the same point. The angle between the paths at this point is illustrated and equal to $\theta$.
Figure 4.5: The angle between two paths in the complex plane, at the point where they meet.

Theorem 4.2 Suppose two paths in the complex plane, \(\gamma_1(t)\) and \(\gamma_2(t)\), meet at the point \(\gamma_1(0) = \gamma_2(0) = 0\), with angle \(\theta\). Suppose also that \(f\) is a holomorphic function with non-zero derivative at \(z = 0\). Then the angle between the transformed paths, \(f \circ \gamma_1(t)\) and \(f \circ \gamma_2(t)\) at the point they meet (i.e. \(f(0)\)) is also \(\theta\).

Proof. The tangent to the path \(\gamma_1(t)\) at \(t = 0\) is the derivative \(\gamma_1'(0)\). This makes an angle with the positive real axis of \(\arg\gamma_1'(0)\). The angle between the two paths must therefore be \[ \theta = \arg\gamma_1'(0) - \arg\gamma_2'(0) = \arg\left(\frac{\gamma_1'(0)}{\gamma_2'(0)}\right). \]

If we consider the transformed paths, we can calculate the angle between them in the same way, to get \[ \theta' = \arg\left(\frac{(f \circ \gamma_1)'(0)}{(f \circ \gamma_2)'(0)}\right). \] We can apply the chain rule to the contents of the brackets, \[ \frac{(f \circ \gamma_1)'(0)}{(f \circ \gamma_2)'(0)} = \frac{f'(0)\gamma_1'(0)}{f'(0)\gamma_2'(0)} = \frac{\gamma_1'(0)}{\gamma_2'(0)}, \] (where the last step is possible only when \(f'(0) \neq 0\)). Hence \[ \theta' = \arg\left(\frac{(f \circ \gamma_1)'(0)}{(f \circ \gamma_2)'(0)}\right) = \arg\left(\frac{\gamma_1'(0)}{\gamma_2'(0)}\right) = \theta. \]

Note that the theorem above makes applies some strict conditions: the meeting point of the paths must be at zero and both paths must be at that point when \(t = 0\). However, I hope you can see that these conditions are not essential. Two paths that meet at \(z \neq 0\) can always be translated in the complex plane so that the meeting point is at zero, while the paths can always be reparameterised so that they meet when \(t = 0\) for both paths.

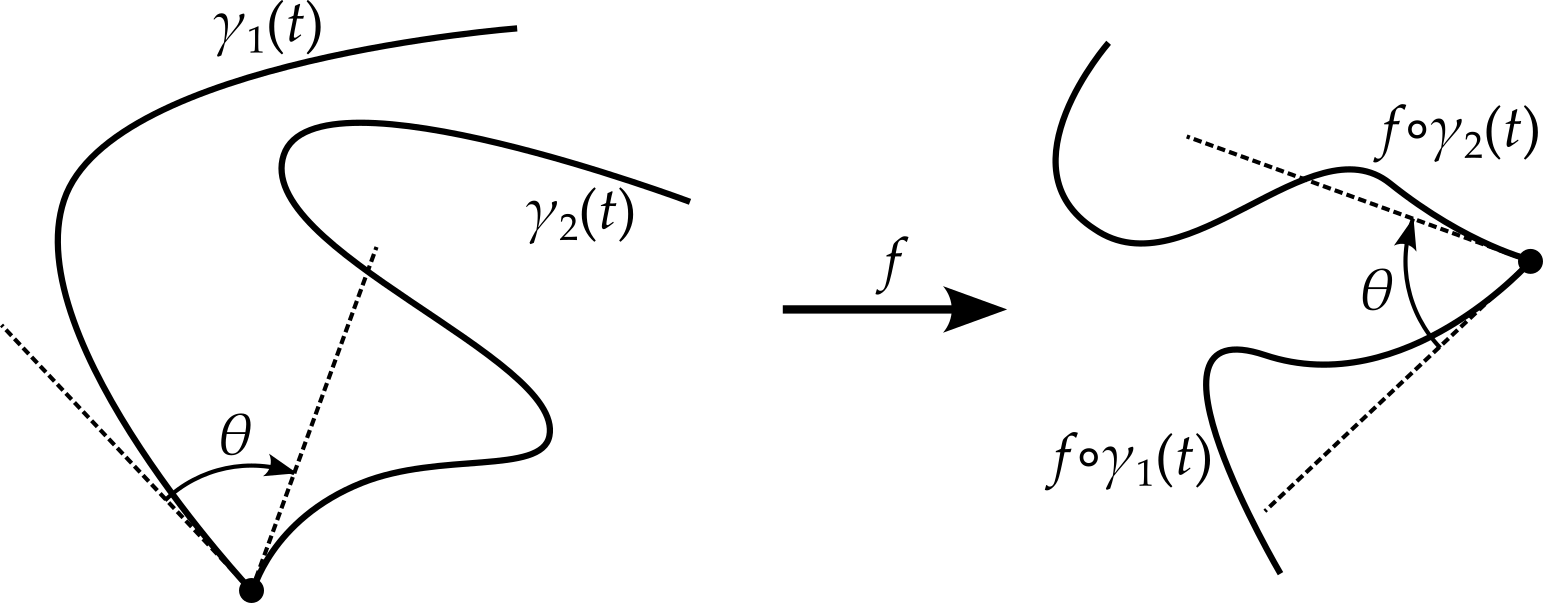
The left side of the diagram shows the same two paths as before, starting from a point with an angle of $\theta$ between them. The right hand side shows how the paths might transform. The angle between the paths at the start point is illustrated in each case and shown to be equal.
Figure 4.6: The holomorphic function \(f\) transforms the two paths. While the shape of the paths may change, the angle between two paths where they meet is preserved. (The derivative of \(f(z)\) at the highlighted point is assumed to be non-zero.)

A corollary to this is that if \(f = u + iv\) is a holomorphic function, then lines of constant \(u\) cross lines of constant \(v\) at right angles, since these lines are mapped to vertical and horizontal lines by the function \(f\). This can be proved in a different way.

Proof. Recall that the gradient of a function \(u\) is perpendicular to contours of constant \(u\). Therefore, if we can show that the gradient of \(u\) is perpendicular to that of \(v\), then we will show that contours of constant \(u\) are perpendicular to contours of constant \(v\). Well \[ \begin{split} \nabla u . \nabla v &= \begin{pmatrix} \partial_x u\\ \partial_y u \end{pmatrix} . \begin{pmatrix} \partial_x v\\ \partial_y v \end{pmatrix} = \partial_xu\partial_xv + \partial_yu\partial_yv\\ &= -\partial_xu\partial_yu + \partial_yu\partial_xu = 0, \end{split} \] where we use the Cauchy-Riemann equations to get to the second line.

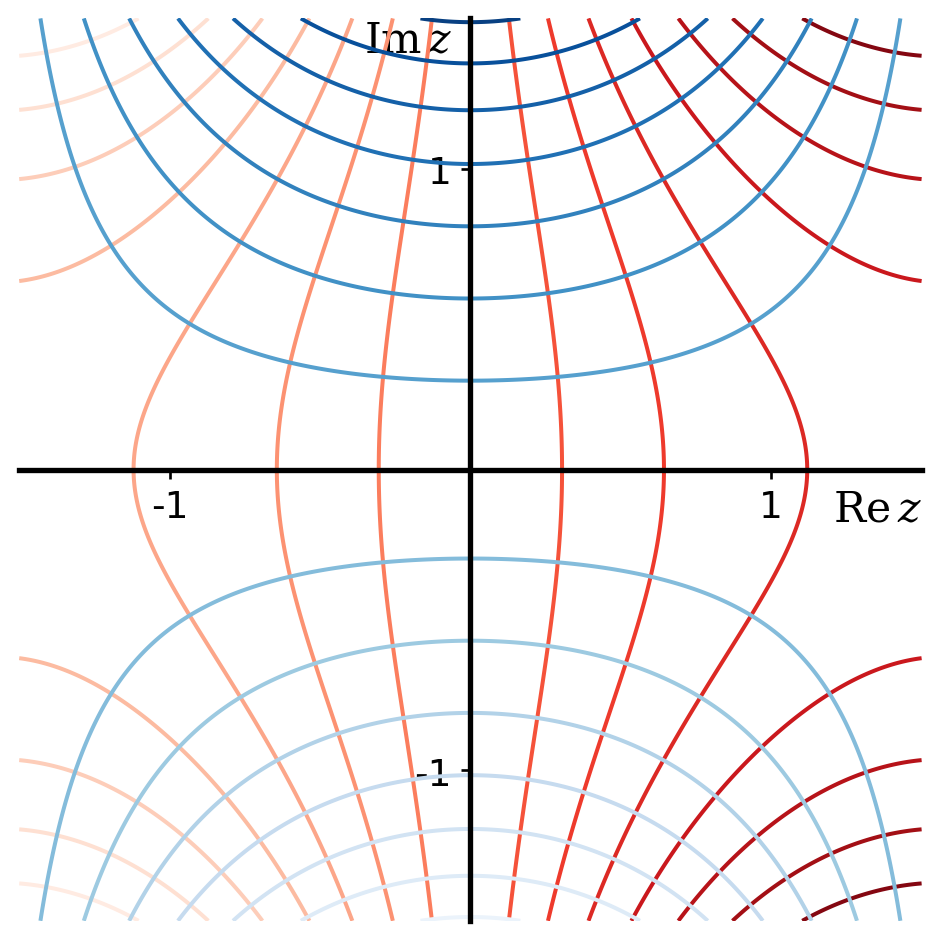
Lines in different shades of red show contours of constant $u$, while lines in blue show contours of constant $v$. At the many points at which these contours cross each other, the angle of crossing can be seen to always be ninety degrees.

Lines of constant \(u\) (in red) and \(v\) (in blue) for the holomorphic function \(f(z) = u(z) + iv(z) = \sin z\). Notice how the contours cross each other at right angles. (The region has been chosen to ensure that the derivative is never zero.)

The complex function \(f(z) = z^2\) is holomorphic in all of \(\mathbb{C}\), but the derivative is zero when \(z = 0\). Confirm that the contours where \(\operatorname{Re}z^2\) is constant cross those where \(\operatorname{Im}z^2\) is constant at right angles, except at \(z = 0\). What happens to the contours at \(z = 0\)?

Let \(u\) and \(v\) be the real and imaginary parts of \(z^2\). Then since \(z^2 = (x + iy)^2 = x^2 - y^2 + 2ixy\), we have \(u = x^2 - y^2\) and \(v = 2xy\). We can plot the lines \(u = x^2 - y^2 = \text{const}\) and \(v = 2xy = \text{const}\) - you should recognise that both of these will produce hyperbolas, but with different orientations, as shown below.

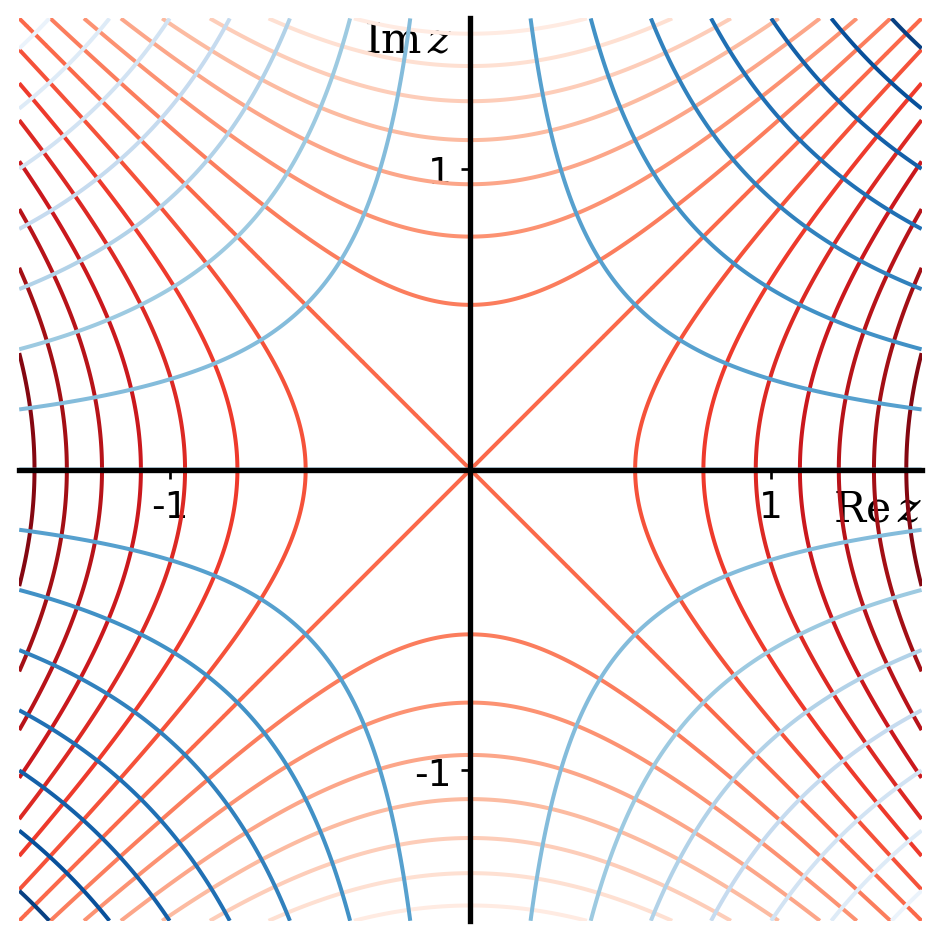
Lines of constant $u$, shown in different shades of red, form hyperbolas that are aligned vertically or horizontally, while lines of constant $v$ form hyperbolas aligned on the diagonals, i.e. like the graph of $y = 1/x$. Again at the points at which these contours cross each other, the angle of crossing can be seen to be ninety degrees, except at the origin.

Lines of constant \(u\) (in red) and \(v\) (in blue) for the holomorphic function \(f(z) = u(z) + iv(z) = z^2\). Again, contours cross each other at right angles, except at \(z = 0\).

The contours do cross at right angles, except at the origin. Here, the contours \(x^2 - y^2 = 0\) form a diagonal cross, while the contours \(2xy = 0\) (not shown) are the real and imaginary axes.

4.7 Real versus complex differentiability - a recap

When the definition of the complex derivative was introduced above, you might have wondered why we were making such a fuss - the definition looks the same as that for the real derivative. And yet the fact that the limit is taken in the complex plane and must be the same in any direction makes holomorphic functions seem curiously straighjacketed.

Compare with real differentiable functions. Draw any smooth graph, continuous and without kinks, and you have a real differentiable function. Holomorphic functions are much more seriously constrained. The real part of a holomorphic function must not only vary ‘smoothly’, but also satisfy Laplace’s equation - i.e. be a harmonic function. Once we have the real part, we have even less choice about how the imaginary part behaves - it not only must satisfy Laplace’s equation, but must be precisely chosen so as to produce contours that cross those of the real part at right angles9.

9 Or alternatively, it must be chosen so as to ensure that the Cauchy-Riemann conditions are satisfied.

10 There may be some isolated points where the function fails to be differentiable, or the function might fail to be holomorphic everywhere for more interesting reasons

Is this bad news? Not at all. While we might expect to find few functions that satisfy these stringent conditions, as it happens most of the functions we are familiar with are holomorphic over most of the complex plane10. Moreover, we can think of these ‘stringent conditions’ as useful properties instead, that allow us to prove useful results. Indeed, we will discover that some of these results can greatly simplify seemingly complicated tasks, in particular, integration.