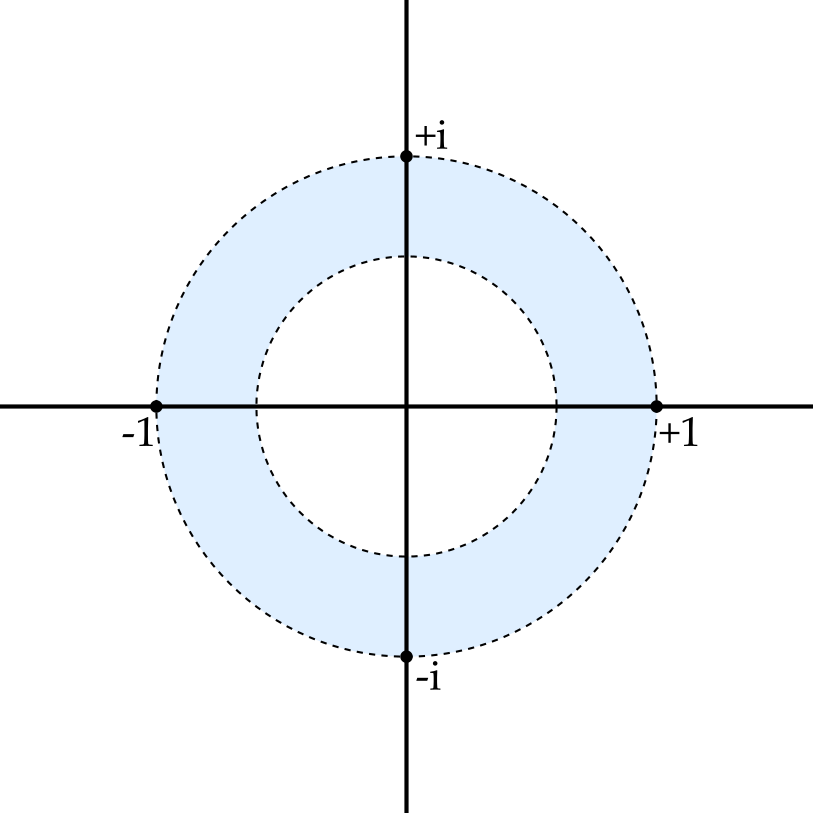
Some topological notions – Introduction to Complex Analysis

Topology? I thought we were learning Complex Analysis!

Indeed we are. However, I will inevitably discuss regions of the complex plane, or neighbourhoods of a point and these are both notions from topology that often feature in a course on Complex Analysis.

For this unit, you can manage with only a vague, intuitive notion of what regions and neighbourhoods are, so reading this document is entirely optional — I will not be testing you on this in the exams. However, some of you may be interested in seeing more precise definitions of these notions.

Open disc

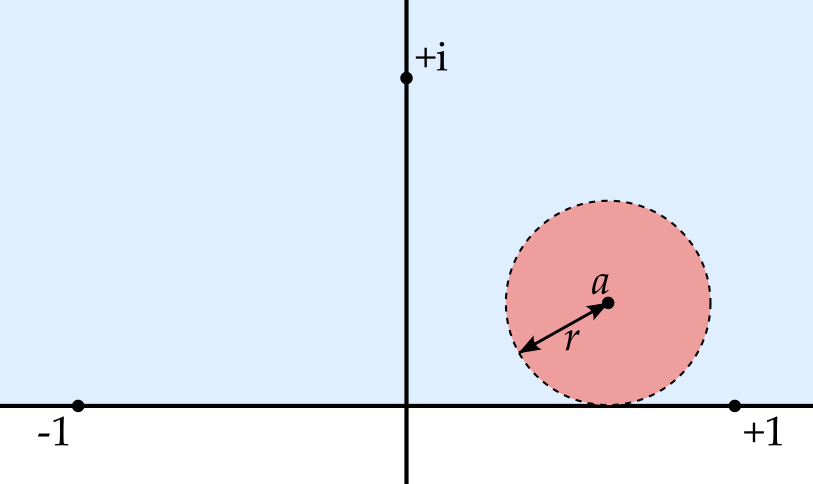
The open disc, \(\mathrm{D}(a; r)\), where \(r > 0\), is the set of points at a distance less than \(r\) from point \(a\), i.e. \[\mathrm{D}(a; r) = \left\{x : \left|x - a\right| < r\right\}.\] In one dimension, i.e. in \(\mathbb{R}\), this is just an open interval, e.g.

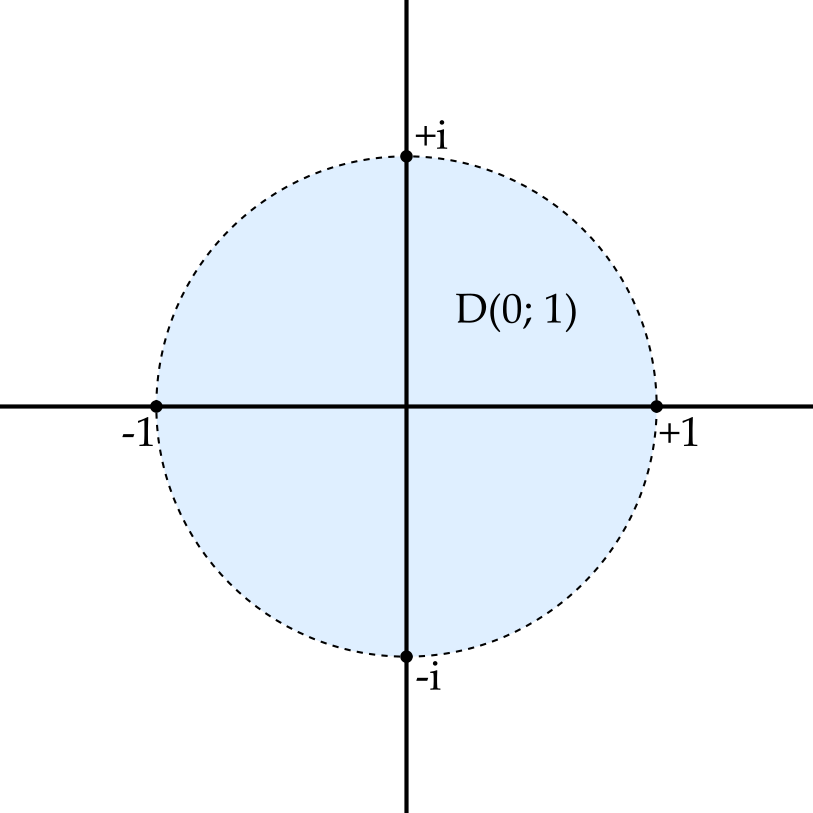
\[\mathrm{D}(0; 1) = (-1, 1).\]

In two dimensions, e.g. in \(\mathbb{C}\), we get something closer to our everyday notion of a disc — the inside of a circle, not including the boundary.

In three dimensions, a ‘disc’ is the interior of a sphere, and so on. However, for this course we will work almost exclusively in the two dimensions of the complex plane.

There are two related types of disc. The closed disc is one that includes its boundary, i.e. \[\overline{\mathrm{D}}(a; r) = \left\{x : \left|x - a\right| \leq r\right\}.\] Meanwhile, the punctured disc is the open disc but without the central point, i.e. \[\mathrm{D'}(a; r) = \left\{x : 0 < \left|x - a\right| \leq r\right\}.\]

Open set

A subset \(S\) of a space (e.g. \(\mathbb{R}\) or \(\mathbb{C}\)) is open if, for every point \(s \in S\), we can find \(\epsilon > 0\) such that \(\mathrm{D}(s; \epsilon) \subseteq S\). In other words, for every point in \(S\), we can move at least a little bit in any direction and remain within the set \(S\). No point in \(S\) is on the ‘edge’.

Examples:

The open interval (0, 1) is open in \(\mathbb{R}\). Consider any \(a \in (0, 1)\) and let \(r = \min(a, 1 - a)\). Then \(\mathrm{D}(a; r) \subseteq (0, 1)\).

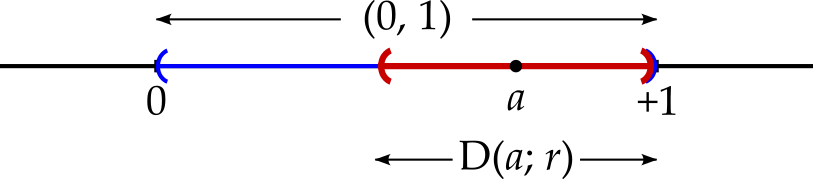
\(\mathrm{D}(a; r)\) lies in \((0, 1)\).

Proof

We want to show that any point in \(\mathrm{D}(a; r)\) is also in \((0, 1)\). Suppose that \(s \in \mathrm{D}(a; r)\), so that \(\left|s - a\right| < r\). Using the triangle inequality, we find that \[\left|s\right| = \left|s - a + a\right| \leq \left|s - a\right| + \left|a\right| < r + a.\] But we also know that \(r \leq 1 - a\) and so \(\left|s\right| < 1\) and \(s < 1\). Similarly \[\left|1 - s\right| = \left|1 - a + a - s\right| \leq \left|1 - a\right| + \left|a - s\right| < 1 - a + r,\] via the triangle equality. Since \(r \leq a\), this gives \(\left|1 - s\right| < 1\) and so \(s > 0\). Hence, if \(s \in \mathrm{D}(a; r)\) then it also belongs to \((0, 1)\).
The open disc, \(\mathrm{D}(0; 1)\) is open in \(\mathbb{C}\). Suppose that \(a\) is any point in \(\mathrm{D}(0; 1)\) and write \(a = se^{i\theta}\). Note that \(s < 1\). Then if we set \(r = 1 - s\), we see that \(\mathrm{D}(a; r) \subseteq \mathrm{D}(0, 1)\).

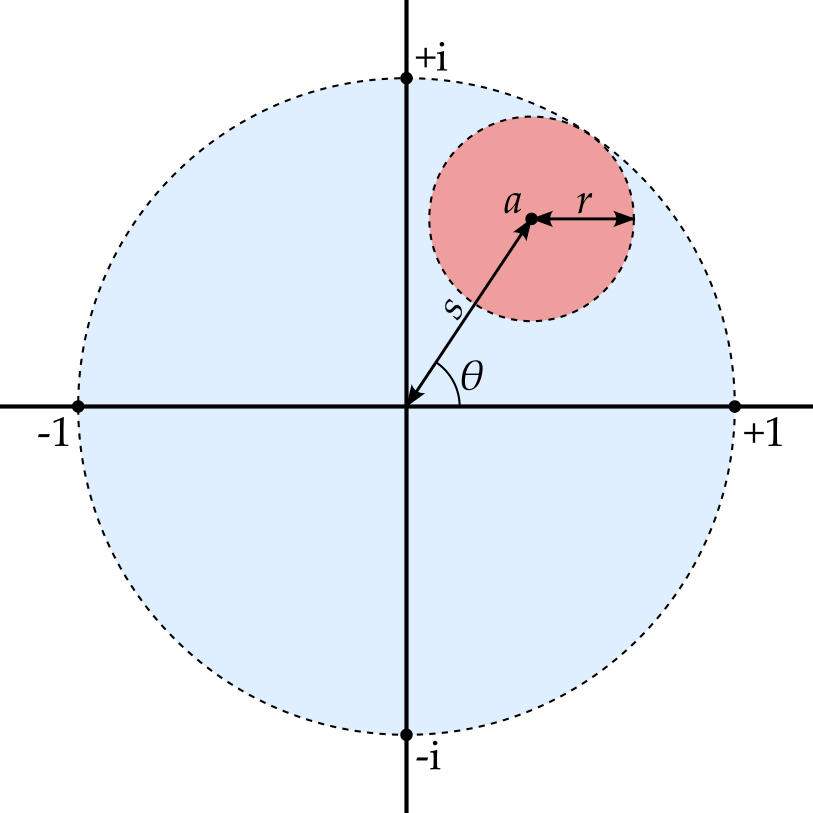
\(\mathrm{D}(a; r)\) lies in \(\mathrm{D}(0, 1)\)

Proof

If \(x \in \mathrm{D}(a; r)\) then \[\left|x\right| = \left|x - a + a\right| \leq \left|x - a\right| + \left|a\right| < r + s = 1\] and so \(x \in \mathrm{D}(0; 1)\).
The (open) upper half plane, defined by \(U = \left\{z \in \mathbb{C} : \operatorname{Im}z > 0\right\}\) is open.

The upper half plane.

Proof

An exercise. The diagram above may help.
The closed interval, \([0, 1]\) is not open. Consider \(a = 1 \in [0, 1]\). Any open disc \(\mathrm{D}(1; r)\) (where \(r > 0\)) must contain points not in \([0, 1]\), e.g. \(1 + \frac{r}{2}\).

\(\mathrm{D}(1; r)\) cannot be inside \([0, 1]\), no matter how small \(r > 0\) is.

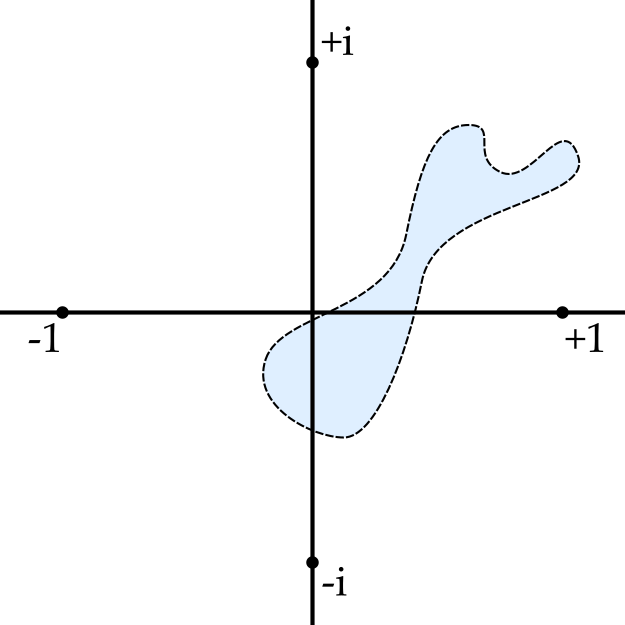
\(r\) is simply the shortest distance from \(a\) to the boundary

Region

A region in \(\mathbb{C}\) is a non-empty, connected, open subset of \(\mathbb{C}\). (I will not define connectedness here, but will assume that you can usually recognise a connected set when you see one.)

Neighbourhood

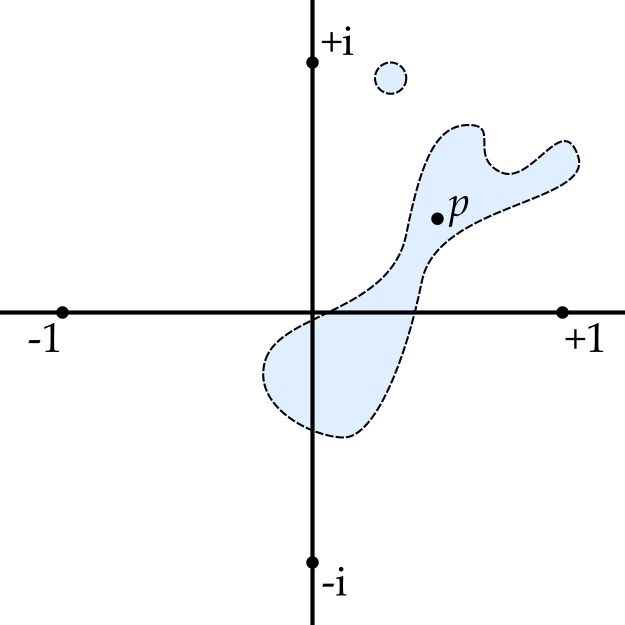
There are two commonly used definitions for a neighbourhood in \(\mathbb{C}\) of a point \(p\).

An open set \(V \subseteq \mathbb{C}\) that contains \(p\).
A set \(V \subseteq \mathbb{C}\) that contains an open set \(U\) that contains \(p\).

In this course, it will make little difference which definition we use. The important thing is that one can move at least a little way, in any direction, from point \(p\) without leaving the neighbourhood.

Limit points

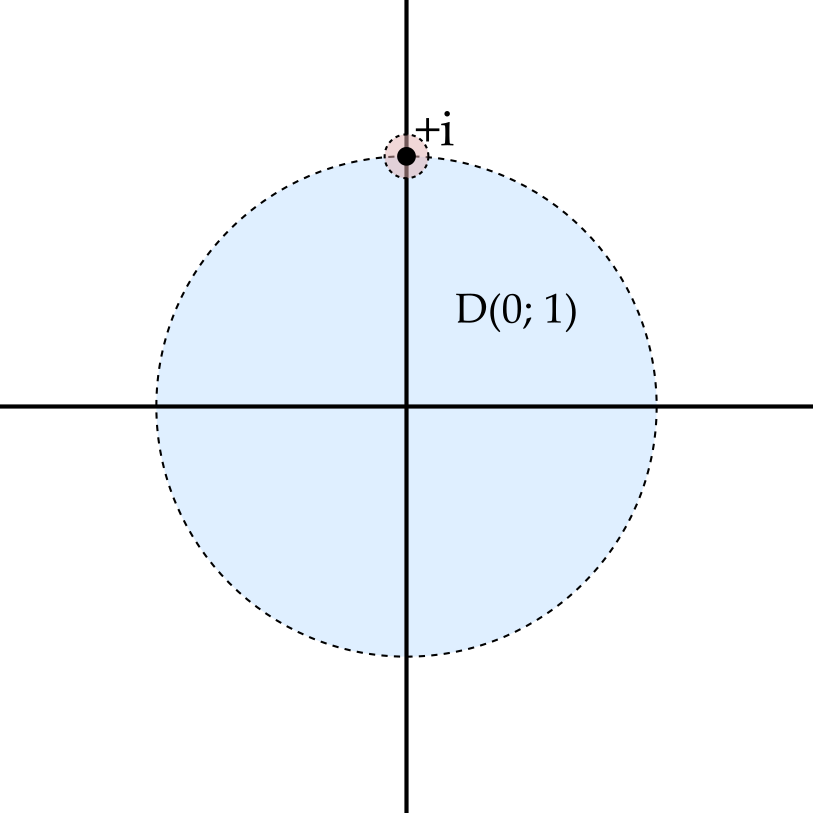
Suppose \(S\) is a subset of \(\mathbb{C}\). Then \(z \in \mathbb{C}\) is a limit point of \(S\) if every neighbourhood of \(z\) contains points other than \(z\) that belong to \(S\).

Notice that a limit point of \(S\) need not be a member of \(S\). For example, while \(i\) is not a member of the unit disc \(\mathrm{D}(0; 1)\), it is a limit point.

The point \(z = i\) is not in \(S = \mathrm{D}(0; 1)\) but is limit point of \(S\). Notice how any neighbourhood of \(i\), such as the small disc shown, must overlap with \(S\).

Meanwhile, a member of \(S\) need not be a limit point. If \(S = \mathrm{D}(0; 1) \cup \{2\}\), then \(2 \in S\) but \(z = 2\) is not a limit point. Such points are called isolated points of \(S\).

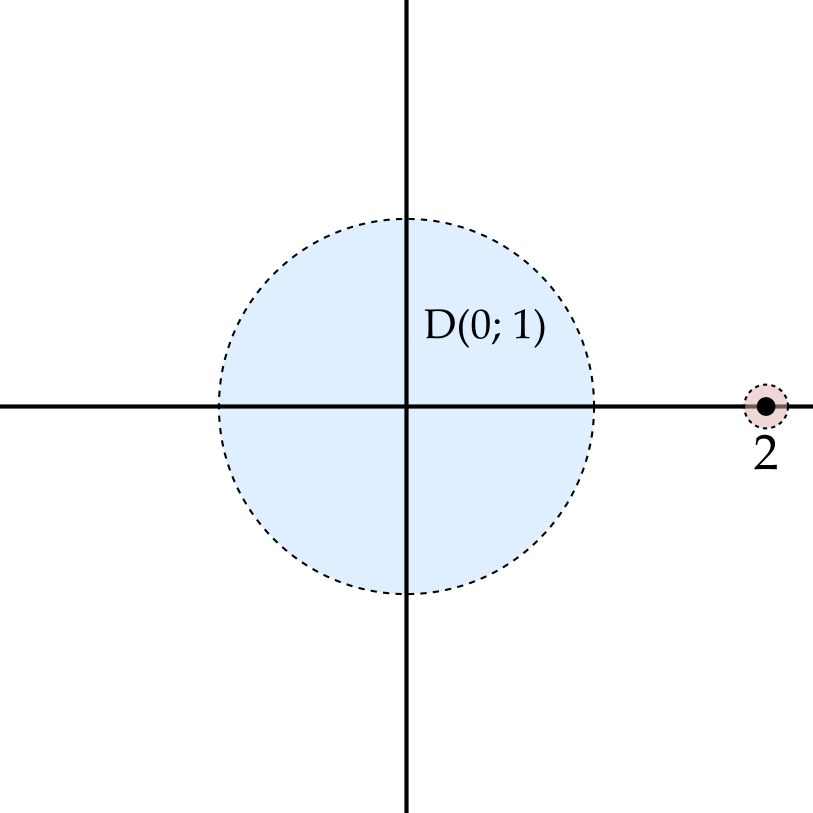
The point \(z = 2\) is in \(S = \mathrm{D}(0; 1) \cup \{2\}\) but is not a limit point of \(S\). The small disc shown contains no points in \(S\) other than \(z = 2\).

An alternative but equivalent definition is that \(z\) is a limit point of \(S\) if \(\mathrm{D'}(z; r) \cap S \neq \emptyset\) for every \(r > 0\).

Simply connected versus multiply connected

Since we will never work in more than two dimensions in this course, it is sufficient to think of a simply connected region as being a region without holes. Hence a disc is simply connected, while an annulus, e.g. \(\left\{z \in \mathbb{C} : 0.6 < \left|z\right| < 1\right\}\), is not.