What you should already know
Hopefully, all of the following is already familiar to you. If not, make sure to revise the relevant material from your first-year mathematics course.
If you need further help with the basics of complex numbers, I have also provided more detailed notes in the next appendix. While I have referred to this as ‘chapter zero’ of the unit, I will not cover this material in lectures, but will assume that you know it.
Complex Numbers
If \(z = x + iy\) then
- \(\operatorname{Re}z = x\)
- \(\operatorname{Im}z = y\)
The modulus, \(\left|z\right| = \sqrt{x^2 + y^2}\), is the length of the line from the origin to the number on the Argand diagram (see below). The argument, \(\arg z\) is the angle this line makes with the positive real axis. You should know that calculating the argument requires care, but that a starting point is to calculate \(\arctan\frac{y}{x}\).
If \(r = |z|\) and \(\theta = \arg z\), we can write \(z = re^{i\theta} = r(\cos\theta + i\sin\theta).\)
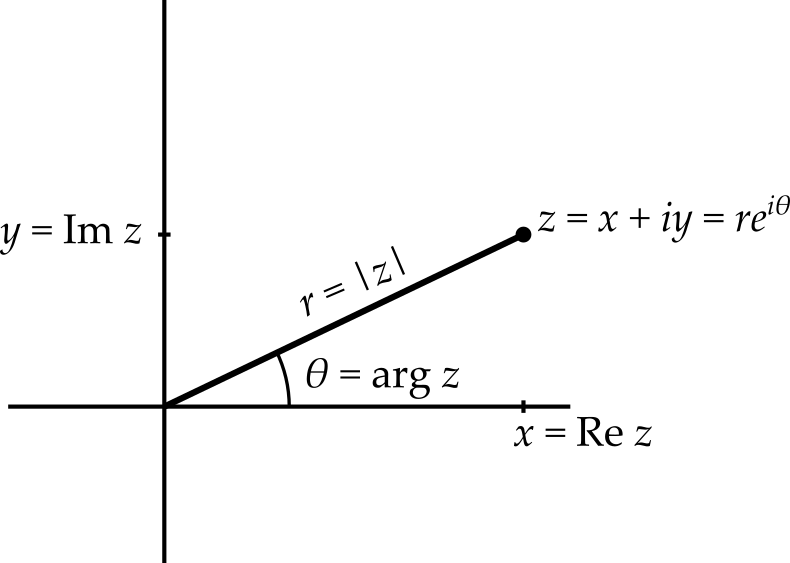
You should be able to add and subtract complex numbers in Cartesian form (\(x + iy\)), multiply and divide complex numbers in either Cartesian or polar form (\(re^{i\theta}\)) and be able to convert between the two forms. You should also be able to find powers, \(z^n\) and roots, \(z^{1/n}\), of complex numbers (where \(n\) is an integer) and be aware that, when taking roots, there are multiple valid answers.
Also, if \(z = x + iy\) then
- \(z^* = x - iy\)
- \(\operatorname{Re}z = \frac{1}{2}(z + z^*)\)
- \(\operatorname{Im}z = \frac{1}{2i}(z - z^*)\)
- \(|z|^2 = z^*z\)
You should be able to find the complex conjugate of expressions, e.g. to simplify \((iuv + w/z)^*\), where \(u\), \(v\), \(w\) and \(z\) are all complex.
You should understand why, for any complex numbers \(w\) and \(z\), it is true that \(|w + z| \leq |w| + |z|\). (Triangle inequality.)
Derivatives
You should understand the difference between partial derivatives and ordinary derivatives and be confident in calculating them.
Functions
You should know the Taylor series for \(e^x\), \(\sin x\) and \(\cos x\), i.e.
\[ \begin{split} e^x = & \sum_{n = 0}^{\infty} \frac{x^n}{n!} &&= 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \ldots\\ \sin x = & \sum_{n = 0}^{\infty} \frac{(-1)^n}{(2n + 1)!}x^{2n + 1} &&= x - \frac{x^3}{3!} + \frac{x^5}{5!} - \ldots\\ \cos x = & \sum_{n = 0}^{\infty} \frac{(-1)^n}{(2n)!}x^{2n} &&= 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \ldots \end{split} \]
Series
You should know the formula for the sum of a geometric series, i.e. \[ \sum_{n = 0}^\infty r^n = \frac{1}{1 - r}. \] You should know what it means for a series to be divergent, convergent, absolutely convergent or conditionally convergent and know examples of such series. You should also be familiar with convergence tests, in particular the comparison test and the ratio test. Recall that this involves calculating \[ \lim_{n \rightarrow \infty}\left|\frac{a_{n + 1}}{a_n}\right|. \]
- If this is less than one, the series \(\sum_{n=0}^\infty a_n\) converges (absolutely).
- If more than one, the series diverges.
- If equal to one then the test in inconclusive.