Chapter 0: Revision of complex numbers

Introduction

This ‘chapter zero’ of the lecture notes contains material that (mostly) will not be covered in lectures. You should have seen this material before in your first-year mathematics unit, but I realise that some of you may wish to revise the basics of complex numbers, so provide this chapter in the hope that it will be helpful.

You will already have seen applications of complex numbers in physics, for example when considering oscillating systems or electrical impedance in AC circuits or, most notably, in quantum mechanics. The many applications of complex numbers should, I hope, provide sufficient motivation to study how they work.

A new number

Since before school, we are introduced to a growing collection of numbers. Starting with the set of natural numbers, \(\mathbb{N}\), that we count objects with, we proceed to add negative numbers to our collection, to produce the set of integers, \(\mathbb{Z}\). Adding fractions then produces the set of rational numbers, \(\mathbb{Q}\), yet since this still does not include numbers like \(\sqrt{2}\) and \(\pi\), we augment our collection still further to obtain the set of real numbers, \(\mathbb{R}\)¹.

¹ Defining \(\mathbb{R}\) is actually rather tricky, but hopefully you are happy with the notion of the real numbers represented as a line (the real line) with no ‘gaps’.

² There is no reason such a number should exist, but we play along to see what happens

We will now proceed to add to our collection yet another new number², \(i\), defined to satisfy \(i^2 = -1\). So far, this is rather unimpressive and inventing a solution to an equation that we couldn’t previously solve feels like cheating. However, suppose that we also insist that we should be able to add and multiply \(i\) with ordinary real numbers and that addition and multiplication should continue to follow the rules we are used to. Now we will find that the invention of this single number has far-reaching consequences.

Imposing these rules immediately results in the creation of further new numbers³ like \(2i\), \(4 + i\) and \(2i - 6\). Our new set of numbers now includes all numbers of the form \(x + yi\), where \(x\) and \(y\) are real. We call this set the complex numbers, \(\mathbb{C}\). We will see later that not only does \(\mathbb{C}\) include a solution to \(x^2 = -1\), but that it contains solutions to all polynomial equations and many other equations that were previously unsolveable such as \(e^x = -1\) and \(\cos\theta = 2\).

³ These must be new, if addition and multiplication follow the normal rules. For example, \[(2i)^2 = 4i^2 = -4\] and neither \(i\) nor any real number, when squared, gives minus four.

Parts of a complex number

If \(z = x + yi\) then we call \(x\) the real part of \(z\) and \(y\) the imaginary part. In symbols, \(\operatorname{Re}z = x\) and \(\operatorname{Im}z = y\). If \(\operatorname{Re}z = 0\) then \(z\) may be called an imaginary number⁴

⁴ This is somewhat unfortunate terminology, as it leads some to think of \(i\) as being less valid, in some way, than real numbers such as \(\sqrt{2}\) or \(-4\).

The complex conjugate

The complex conjugate, \(z^*\), of a complex number, \(z\), is found by flipping the sign of the imaginary part. In other words, if \(z = x + yi\), where \(x\) and \(y\) are both real numbers, then \(z^* = x - yi\).⁵

⁵ You will also see the alternative notation, \(\overline{z}\), used for the complex conjugate of \(z\).

Now that we have defined the complex conjugate, the following formulae for the real and imaginary part of a complex number are sometimes useful

\[ \begin{aligned} \operatorname{Re}z &= \frac{1}{2}(z + z^*)\\ \operatorname{Im}z &= \frac{1}{2i}(z - z^*) \end{aligned} \]

Exercise

Check that these formulae really do work for a general complex number \(z\). (You may want to look at the rules for addition and subtraction below.)

Solution

Let \(z = x + yi\). Then \(z^* = x - yi\) and so \[z + z^* = x + yi + x - yi = 2x = 2\operatorname{Re}z.\] Dividing by two now gives \(\operatorname{Re}z = \frac{1}{2}(z + z^*)\)

Similarly, \[z - z^* = x + yi - x + yi = 2yi = 2i\operatorname{Im}z.\] Dividing by \(2i\) now gives \(\operatorname{Im}z = \frac{1}{2i}(z - z^*)\).

Arithmetic

Remember, addition and multiplication should follow all the rules that we are used to. So…

Addition and subtraction

\[(a + bi) + (c + di) = (a + c) + (b + d)i.\] So, for example, \[(1 + 2i) + (3 - 4i) = 1 + 3 + (2 - 4)i = 4 - 2i.\]

Here we have used the rules that state that the order in which addition occurs does not affect the result⁶.

⁶ Commutativity and Associativity

Subtraction, is similar, for example \[(1 + 2i) - (3 - 4i) = 1 - 3 + (2 + 4)i = -2 + 6i.\]

Multiplication

Multiplying out the brackets, we get \[(a + bi)(c + di) = ac + adi + bci + bdi^2 = (ac - bd) + (ad + bc)i.\] For example \[(1 + 2i)(3 - 4i) = 3 + 6i - 4i - 8i^2 = 11 + 2i.\]

Exercise

Simplify \((1 + 2i)(1 - 2i)\).

Solution

Multiplying out the brackets, we get \((1 + 2i)(1 - 2i) = 1 - (2i)^2 = 1 + 4 = 5\). So in this case, we have multiplied two complex numbers together and obtained a real number.

Division

We would like to write \((a + bi) / (c + di)\) in the standard form, \(x + yi\), where both \(x\) and \(y\) are real. It is not immediately obvious how to do this — will we need to introduce even more new numbers? Thankfully not! Multiply both the top and the bottom of the fraction by the complex conjugate of the denominator, \[\frac{a + bi}{c + di} = \frac{(a + bi)(c - di)}{(c + di)(c - di)} = \frac{(ac + bd) + (bc - ad)i}{c^2 + d^2} = \frac{ac + bd}{c^2 + d^2} + \frac{bc - ad}{c^2 + d^2}i,\] and we have a result in the required form.

Example 1 \[\frac{1}{1 + i} = \frac{1 - i}{(1 + i)(1 - i)} = \frac{1 - i}{2} = \frac{1}{2} - \frac{1}{2}i.\]

Example 2 \[\frac{1 + i}{1 - i} = \frac{(1 + i)^2}{(1 - i)(1 + i)} = \frac{2i}{2} = i.\]

Exercise

Simplify \((1 + 7i) / (3 + i)\).

Solution

Multiplying top and bottom by \(3 - i\), we get \[\frac{1 + 7i}{3 + i} = \frac{(1 + 7i)(3 - i)}{(3 + i)(3 - i)} = \frac{10 + 20i}{10} = 1 + 2i.\]

Complex conjugation revisited

The operations of addition, subtraction, multiplication and division interact with each other exactly as one would expect from our experience of using them with real numbers. However, adding the operation of complex conjugation gives us some new rules. \[ \begin{aligned} (w + z)^* &= w^* + z^*\\ (w - z)^* &= w^* - z^*\\ (wz)^* &= w^*z^*\\ \left(\frac{w}{z}\right)^* &= \frac{w^*}{z^*} \end{aligned} \] In short, the complex conjugate of an expression is obtained by taking the complex conjugate of each of its parts, e.g. \[\left(\frac{ixz^2}{y^*}\right)^* = \frac{-ix^*(z^*)^2}{y}.\] In the denominator here, we have used the fact that \((y^*)^* = y\), i.e. taking the complex conjugate twice returns the original number.

Visualising complex numbers: The Argand diagram

Thus far, we have been thinking about complex numbers algebraically. It is also useful to think of them visually. The fact that each complex number includes two independent components, the real part and the imaginary part, means that complex numbers can be considered either as two dimensional vectors or as positions on the two dimensional plane — the complex plane. A plot of complex numbers on this plane is referred to as an Argand diagram, as shown in figure 1.

Figure 1: Complex numbers plotted on an Argand diagram.

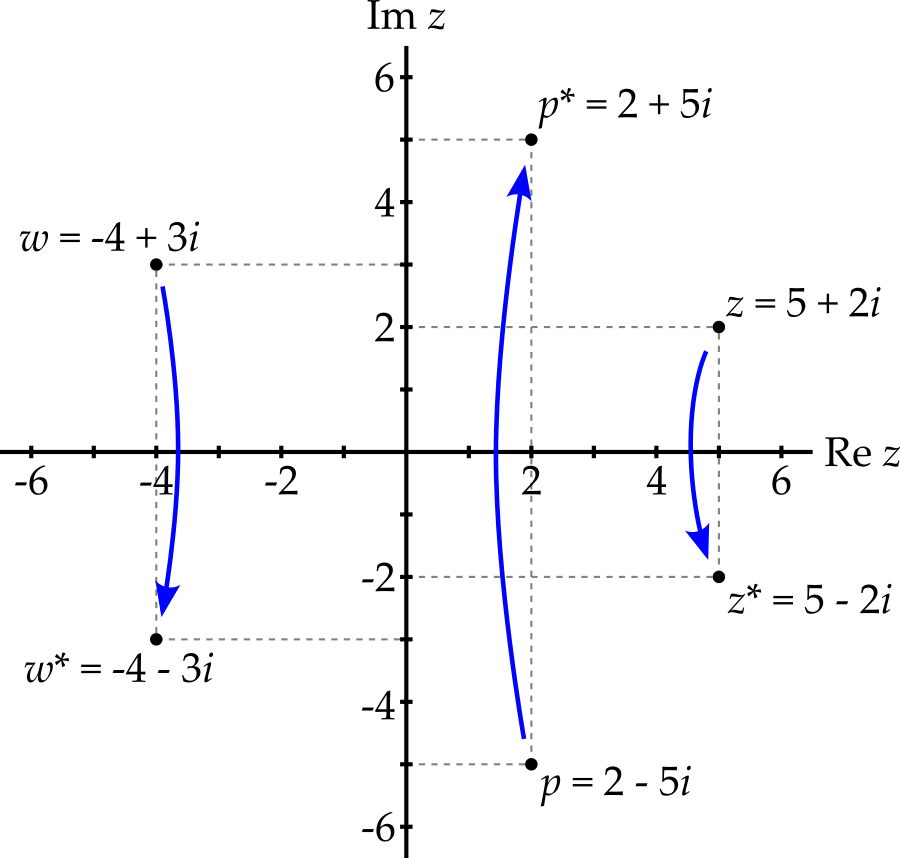
Complex conjugation is now equivalent to a reflection in the real axis, shown in figure 2.

Figure 2: Complex conjugation is reflection in the real axis.

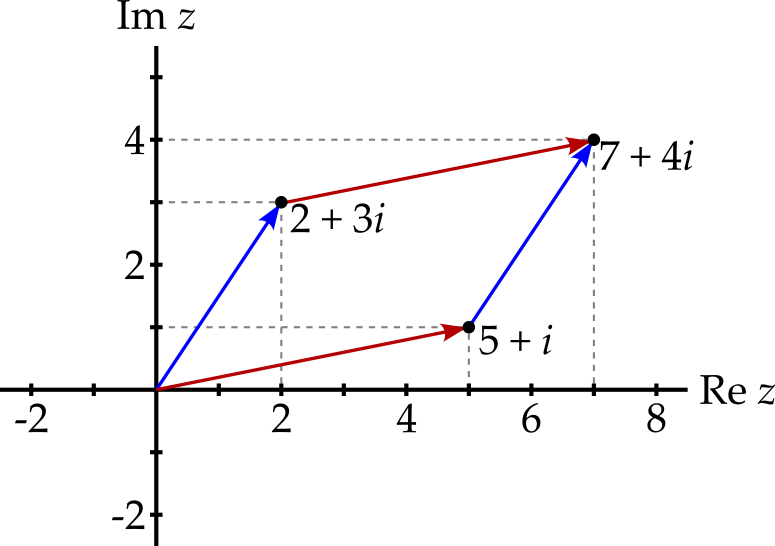
Addition of complex numbers can be visualised as the addition of the 2-dimensional position vectors, as illustrated in figure figure 3.

Figure 3: Visualisation of the addition of complex numbers.

Multiplication, however, is not like multiplication of vectors. Visualisation of the multiplication of complex numbers will have to wait until we have covered the polar representation.

Polar coordinates

Thus far, we have written our complex numbers in Cartesian form — the real and imaginary components are the Cartesian coordinates of the point in the complex plane. Of course, we can use different coordinates to specify the position of a point in the plane, the most common alternative being (of course) polar coordinates. Here \(r\) is the distance of the point from the origin, while we define \(\theta\) to be the angle from the positive real axis, with the positive direction being anticlockwise. This is illustrated in figure 4.

Figure 4: Cartesian and polar representations of a complex number.

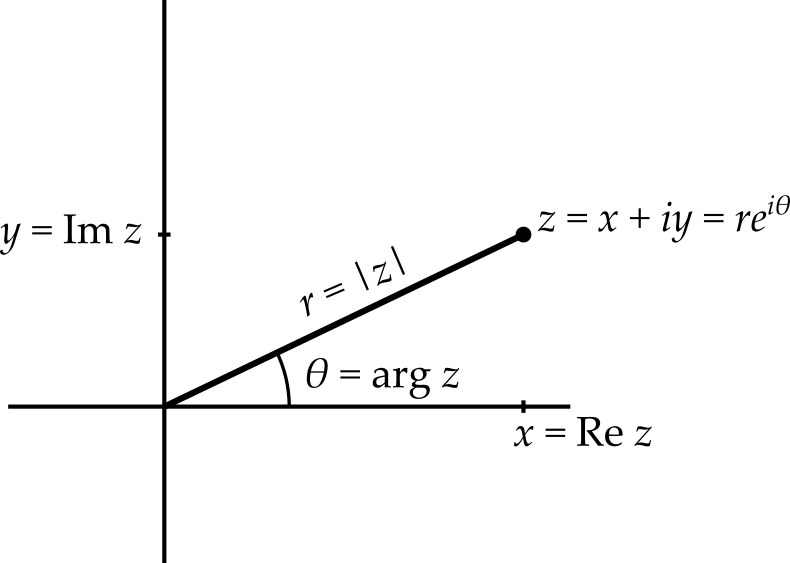
The radial coordinate, \(r\), is called the modulus⁷ of \(z\) and is denoted \(\left|z\right|\) while the angle \(\theta\) is called the argument of \(z\), denoted \(\arg z\). We can relate the various coordinates with some trigonometry, getting

⁷ Alternative names include the magnitude, the absolute value or, if I am being overly casual, simply the size.

• \(x = r\cos\theta\),
• \(y = r\sin\theta\),
• \(r = \left|z\right| = \sqrt{x^2 + y^2} = \sqrt{zz^*}.\)

Exercise

Show that if \(z = x + yi\), then \(zz^* = x^2 + y^2\).

Solution

Start with \[zz^* = (x + yi)(x - yi) = x^2 + xyi - xyi - (yi)^2 = x^2 + y^2.\] (The relationship, \(\left|z\right|^2 = zz^*\) is frequently used and worth remembering.)

Writing the argument in terms of \(x\) and \(y\) is a little trickier. figure 4 would suggest that \(\theta = \arctan{\frac{y}{x}}\) should work, but consider the number \(z = -1 - i\). Here \(\frac{y}{x} = 1\) and if we use a calculator to find the arctangent, we get \(\theta = \frac{\pi}{4}\), i.e. 45 degrees. This clearly does not match the angle in figure 5. The problem is that there are two angles that have a tangent of 1 — we must be careful to choose the right one.

Figure 5: Find the argument of \(z = -1 - i\).

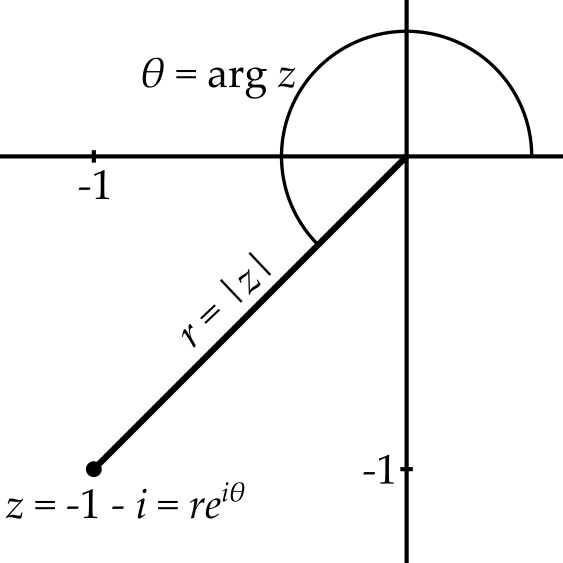
Now if we replace \(x\) with \(r\cos\theta\) and \(y\) with \(r\sin\theta\), we get the polar form of the complex number \[z = r(\cos\theta + i\sin\theta).\] This is fine as far as it goes, but the much more useful useful form is \[z = re^{i\theta}.\] We will soon show that these two expressions are equal, but for just a short while, I ask you to take this on trust.

Visualising multiplication

With this new way of representing complex numbers we can better visualise multiplication on the complex plane. Consider two complex numbers, \(z_1 = r_1e^{i\theta_1}\) and \(z_2 = r_2e^{i\theta_2}\). Then \[z_1z_2 = r_1e^{i\theta_1}r_2e^{i\theta_2} = r_1r_2e^{i(\theta_1 + \theta_2)}.\] In other words, the modulus of the product is just the product of the moduli, i.e. \(r_1r_2\), while the argument of the product is the sum of the arguments of the original numbers, that is \(\theta_1 + \theta_2\). This is illustrated in figure 6.

Figure 6: Multiplication of \(3 + i\) and \(1 + i\) to produce \(2 + 4i\), illustrating how the arguments are added and the modulo multiplied together.

Returning briefly to a more algebraic viewpoint, we have shown that \[ \begin{aligned} \left|z_1z_2\right| &= \left|z_1\right|\left|z_2\right|,\\ \arg(z_1z_2) &= \arg(z_1) + \arg(z_2). \end{aligned} \]

If we consider the operation of multiplying some complex number by \(z = re^{i\theta}\), the operation simply multiplies the modulus by \(r\) and adds \(\theta\) to the argument. We can see the effect of repeatedly performing this operation in figure 7.

Figure 7: Starting with 1, we repeatedly multiply by \(z = re^{i\theta}\). In each multiplication, \(\theta\) is added to the argument of the result, while the modulus is multiplied by \(r\).

Dividing by \(z = re^{i\theta}\) is naturally the opposite of multiplying by \(z\), so that we divide the modulus by \(r\) while \(\theta\) is subtracted from the argument. This can be seen by dividing \(z_1 = r_1e^{i\theta_1}\) by \(z_2 = r_2e^{i\theta_2}\) to get \[ \frac{z_1}{z_2} = \frac{r_1e^{i\theta_1}}{r_2e^{i\theta_2}} = \frac{r_1}{r_2}e^{i(\theta_1 - \theta_2)}. \] In other words \[ \begin{aligned} \left|z_1 / z_2\right| &= \left|z_1\right| / \left|z_2\right|,\\ \arg(z_1 / z_2) &= \arg(z_1) - \arg(z_2). \end{aligned} \]

The complex exponential

Trust only goes so far — it is time to show that \(e^{i\theta} = \cos\theta + i\sin\theta\). But what does \(e^{i\theta}\) mean? We have not yet defined exponentials of complex numbers.

For many useful functions such as \(e^x\), \(\sin x\), \(\cos x\), we know not only their properties but also how to write them as a power series via the Taylor expansion. For example \[ \begin{split} e^x = & \sum_{n = 0}^{\infty} \frac{x^n}{n!} &&= 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \ldots\\ \sin x = & \sum_{n = 0}^{\infty} \frac{(-1)^n}{(2n + 1)!}x^{2n + 1} &&= x - \frac{x^3}{3!} + \frac{x^5}{5!} - \ldots\\ \cos x = & \sum_{n = 0}^{\infty} \frac{(-1)^n}{(2n)!}x^{2n} &&= 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \ldots \end{split} \] We can then use these power series to extend the domain of these function to cover the complex plane.⁸ In other words, we define \(e^z\) (where \(z\) is complex) to be \[ e^z = \sum_{n = 0}^{\infty} \frac{z^n}{n!} = 1 + z + \frac{z^2}{2!} + \frac{z^3}{3!} + \frac{z^4}{4!} + \frac{z^5}{5!} + \ldots. \]

⁸ We can do the same thing with matrices too, to allow us to calculate \(e^A\) or \(\sin B\) where \(A\) and \(B\) are matrices. Here, of course, we will focus on complex numbers!

Now that we have defined \(e^z\), we can expand \(e^{i\theta}\) to get \[ \begin{split} e^{i\theta} &= 1 + i\theta - \frac{\theta^2}{2!} - i\frac{\theta^3}{3!} + \frac{\theta^4}{4!} + i\frac{\theta^5}{5!} - \ldots\\ &= 1 - \frac{\theta^2}{2!} + \frac{\theta^4}{4!} - \ldots + i\left(\theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \ldots\right), \end{split} \] where in the second line we have separated out the real terms and the imaginary terms. But look! The real terms are exactly those for \(\cos\theta\), while \(i\) is multiplied by all the terms for \(\sin\theta\). Hence this simplifies to \[\begin{equation} \tag{Euler's formula} e^{i\theta} = \cos\theta + i\sin\theta \end{equation}\] as desired.